Abstract
The state-space approach (SSA), traditionally utilized in modern control theory, has been successfully adopted over the last three decades to investigate the mechanical behaviors of complex structures composed of composite or smart materials. This is largely due to their increasing application across various fields, including aerospace, civil and marine engineering, and transportation vehicles. This paper provides a comprehensive review of the establishment of state-space formulations for structures of typical configurations, such as beams, plates, shells, and trusses, with a particular focus on their applications in the mechanical analyses of various complex aerospace or smart structures using the transfer matrix method. The paper first summarizes the three-dimensional SSAs applied to laminated structures without any assumptions on physical fields. By employing structural theories such as various beam, plate, and shell theories, simplified one-dimensional and two-dimensional SSAs for laminated structures are developed. The paper then outlines the advances in generating analytical solutions for the mechanical behaviors of laminated structures. For the sake of completeness, the paper also provides an account of SSAs applied to complex periodic structures, particularly in beam and truss forms. To overcome the limitations of conventional SSAs related to structures with specialized geometric configuration or under arbitrary boundary conditions, state-space based numerical methods have been proposed, for example, the state-space based differential quadrature method and state-space based finite-element method. The applications of these methods in the analyses of static and dynamic responses of complex structures are extensively reviewed. It is observed that there are still intriguing and potential research topics for the development of advanced SSAs with enhanced versatility and the studies on practical complex structures used in modern engineering, particularly in aerospace industry. Therefore, this review is expected to be beneficial for researchers in the fields of analytical and numerical methods, composite structures, aerospace, structural engineering, and more.
Introduction
Composite materials typically consist of two or more distinct components, each possessing unique mechanical, electric, magnetic, thermal, or chemical properties. As a result, structures composed of these composite materials, such as laminated structures, often exhibit superior performance characteristics compared to conventional structures made from homogeneous materials. These advantages include lightweight construction, high strength-to-weight and stiffness-to-weight ratios, excellent tailoring properties, and high resistant to corrosion and fatigue [1, 2]. Spacecraft and aircraft are typical weight- and strength-sensitive structures. According to a widely accepted rule of thumb, each pound of weight reduction in a primary structure results in an indirect saving of another pound elsewhere in the aircraft [3]. Today, structures composed of composite materials are increasingly becoming a cornerstone in modern aerospace and aviation industry [4, 5]. Moreover, these complex structures are also finding broader applications in fields such as mechanical and civil engineering, marine, transportation vehicles [6, 7]. Consequently, the burgeoning industrial uses of complex structures have spurred the development and innovation of necessary analytical and numerical techniques for analyzing the mechanical behaviors of these structures [8, 9].
The mechanics of three-dimensional (3D) continua are typically governed by partial differential equations (PDEs), wherein all physical fields, including the displacements, stresses, and strains, are functions of the three spatial coordinate variables and/or the time variable. Consequently, deriving exact analytical solutions for 3D elasticity structures can be challenging. To address this, various structural theories such as rod, beam, plate, and shell theories have been developed, introducing certain assumptions on physical fields regarding their space distributions. These theories have been widely used to study the mechanical behaviors of numerous engineering structures composed of homogeneously isotropic, transversely isotropic, or orthotropic materials. However, these theories sometimes fall short or face significant limitations when predicting the static and dynamic responses of structures composed of composite or smart materials, especially accurate distributions of displacements and stresses at interlayer interfaces. This is due to factors such as strong material anisotropy, multi-field coupling, heterogeneity, and structural complexity. As a result, conventional structural theories often lack the necessary generality and accuracy when studying complex structures.
An alternative strategy involves seeking solutions for complex structures directly based on analytical or numerical methods such as finite element methods (FEMs), displacement and stress functions, Taylor series expansions, and state-space approaches (SSAs), which are the focus of this article. SSAs, traditionally used for modeling control systems, describe the relationships between the output, input, and the state of the system. These three variables are only functions of the time. The state equation of the system is governed by first-order ordinary differential equations (ODEs) with respect to the state and input variables, and the output variables of the system can be fully determined when the state variables are known. By using state-space descriptions, the first-order ODEs of the system are transformed into a matrix expression, thereby enabling efficient utilization of high-performance computer facilities using engineering software such as MATLAB and Mathematica. Furthermore, due to the matrix expression of the system equation, the increase of state variables does not increase the complexity of system descriptions. Thus, SSAs offer better unity of expression and higher computational efficiency than other methods for modeling control systems.
Unlike the first-order ODEs of control systems, the governing equations of a 3D elastic body are PDEs with respect to the selected physical fields such as displacements, stresses, or strains. Therefore, the key to establishing the state-space formulations for elasticity problems lies in selecting the appropriate state variables and transforming the PDEs into a set of first-order ODEs. The practical application of the SSA to elastic bodies dates back to the study on vibrations of non-uniform beams by Thomson in 1950 [10]. By selecting the deflection, rotation, shear force, and bending moment as the state variables, they reformulated the governing equations, the fourth-order ODEs, of the beam deflection as a set of first-order ODEs based on the beam theory. For the non-uniform beam, the layerwise approximate technique (LAT) was employed by them to divide the beam into many segments such that the section of each segment could be treated as constant. Based on state-space descriptions, the continuity conditions at the interfaces and the boundary conditions at the two ends of the beam can be easily expressed by the state variables. Then a transfer relation between the state variables at the two ends of every segment can be established, and a global transfer matrix between the state variables at the two ends of the beam can be finally derived by eliminating all interfacial displacements and tractions based on interlayer continuity conditions. With the increase of the number of the divided segments, the approximate solutions obtained by the SSA approach the exact solutions for free vibration of the non-uniform beam. Evidently, in the SSA the dimensionality of the global transfer matrix of laminated structures is independent of the number and thickness of the layers, and thus the SSA is very powerful and efficient for seeking exact solutions of laminated structures no matter how many layers there are. Furthermore, the displacement and stress components at interlayer interfaces predicted by the SSA are accurately continuous, which cannot be realized by other numerical method like the FEM. Almost simultaneously, Thomson [11] also demonstrated that the SSA could be used for wave propagation analysis in an infinite stratified solid medium. By selecting the particle velocity and stresses as the state variables, the governing equations of the plane wave propagation were transformed into a matrix form, i.e., the state-space formulations for wave motions in a stratified medium.
Building on Thomson’s pioneer work and the increasing use of laminated composite structures, there has been a significant development and application of SSAs in fields such as aerospace, geophysics [12], and structural and civil engineering [6] since 1990s. The 3D state-space formulations for materials with varying material symmetries and multi-field coupling effects, such as transversely isotropic, spherically isotropic, piezoelectric, and magneto-electro-thermo-elastic materials, have all been established for the studies of structures of different geometric configurations and with multi-field couplings. Apart from the general 3D problems, since no assumptions are adopted to simplify the physical fields for the states of plane strain or plane stress, the SSAs applied to solve plane-strain and plane-stress problems are also ascribed to the 3D SSAs as special cases in this article. Leveraging sophisticated structural theories, simplified one-dimensional (1D) and two-dimensional (2D) SSAs have also been developed for the analyses of laminated structures in beam, plate, and shell forms. The mixed SSAs, integrating the transfer matrix method for state vectors and theoretical or numerical methods, have been further developed to predict the mechanical behaviors of complex periodic structures composed of beam or truss units. In addition, various state-space based numerical methods, combining the advantages of SSAs and the associated numerical methods, have been proposed to solve more practical structural problems or address numerical difficulties associated with structures under arbitrary boundary conditions. For instance, in the state-space based differential quadrature method (SS-DQM), the DQM helps to overcome the limitations associated with conventional SSAs for plates and shells with arbitrary boundary conditions, while still retaining the feature of the SSA that the displacement and stress components are accurately continuous at interlayer interfaces. This feature is also inherited by the state-space based finite element method (SS-FEM), making the number of the unknow functions and unknow node variables independent of the layer number of laminated structures, which gives the SS-FEM an edge over conventional FEMs. Other specialized state-space based numerical methods, including the state-space based finite difference method (SS-FDM), state-space based boundary element method (SS-BEM), etc., have also been proposed to deal with structures with certain geometric configurations or to improve the computational efficiency. The overall structural diagram of SSAs applied to complex structures is illustrated in Figure 1.
FIGURE 1
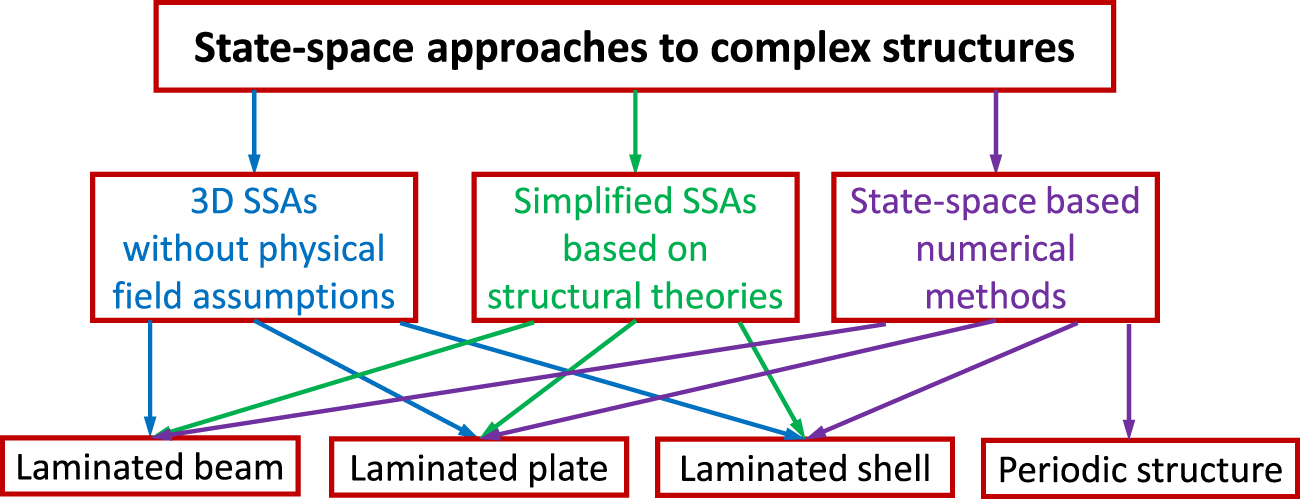
Overall structural diagram of state-space approaches applied to complex structures.
This review aims to highlight the advances of SSAs to structures of typical configurations and their applications in the analyses of mechanical behaviors of complex structures composed of composite or smart materials. We first focus on the 3D SSAs for laminated structures of beam, plate, and shell configurations, in which no assumptions of physical fields are adopted. When structural theories, such as beam, plate, and shell theories, are employed, we present the establishment of 1D and 2D state-space formulations and their extensive applications in the mechanical analyses of laminated structures. We then provide an account of the applications of SSAs in studies on complex periodic structures composed of beam and truss units. The final focus of this article is the advances of state-space based numerical methods and their applications in static and dynamic analyses of complex structures. This review is intended to be beneficial for future studies on advanced SSAs and mechanical behaviors of practical complex structures in various fields, particularly for aeronautical, marine, civil, and transportation applications.
3D State-Space Approaches to Laminated Structures
As previously mentioned, laminated structures have been found extensive applications in fields such as aerospace, aviation, structural engineering, and marine. Despite the flexibility offered by material and structural design and the ability to be composed of numerous layers for carrying large loads, laminated structures often grapple with issues such as the ply delamination and shear destruction due to the low ratio of transverse shear modulus to in-plane modulus. Since 1950s, 3D SSAs, which do not introduce any assumptions on physical fields, have been widely adopted to accurately predict mechanical behaviors of laminated structures. These approaches also provide useful benchmark results for comparing and clarifying various simplified theories or numerical methods. In this section, we will review the advances of 3D SSAs and their applications in analyzing static and dynamic responses of laminated structures of beam, plate, and shell configurations, as summarized in Table 1.
TABLE 1
| Configuration | Mechanical behavior | Reference |
|---|---|---|
| Beam | Bending and vibration | [14–16] |
| Beam | Bending | [6, 17–22] |
| Beam | Vibration | [23] |
| Plate | Bending and vibration | [24–29] |
| Plate | Bending | [30–48] |
| Plate | Vibration | [49–54] |
| Cylindrical shell | Bending, vibration, buckling | [55–57] |
| Cylindrical shell | Bending, vibration | [58–60] |
| Cylindrical shell | Bending | [61] |
| Cylindrical shell | Vibration | [62–68] |
| Cylindrical shell | Buckling | [69] |
| Cylindrical shell | Wave | [70–72] |
| Spherical shell | Bending | [73, 74] |
| Spherical shell | Vibration | [75–77] |
Application of 3D state-space approaches in the mechanical behavior analyses of complex structures of different configurations.
Laminated Beams
Beams, often utilized to represent slender structures with a length significantly greater than their cross-sectional dimensions, are a fundamental component in aeronautical applications. These applications include, but are not limited to, fuselage air wings, helicopter rotor blades, and turbine rotor blades. Laminated beams, in particular, are of paramount importance. This section reviews the research on 3D SSAs for beam configuration as well as their application in the accurate 3D analyses of both static and dynamic responses of laminated beams.
The SSA to elasticity, initially proposed by Bahar for the analysis of 2D plane stress problem in linear elasticity [13], has proven to be a potent and effective tool for deriving exact solutions of elasticity. Utilizing the state-space formulations established for plane-stress problem, Chen et al. [14] presented an exact solution for simply-supported cross-ply laminated beams with interlaminar bonding imperfections, described by a spring-layer model, as shown in Figure 2A. It can be seen from Figure 2B that the transverse shear stress predicted by the 3D SSA for R = 0 was accurately continuous at the interfaces and the imperfect bonding significantly changed its distribution along the thickness direction. Moreover, numerical results indicated that an increase in the imperfection bonding parameter could lead to an increase in deflection and a decrease in the natural frequency, suggesting that interfacial imperfections result in a decrease in the effective stiffness of the laminated beam. The solutions obtained can serve as a valuable benchmark for simplified beam theories or numerical methods proposed for imperfect laminated beams. Chen et al. [6] also employed the SSA to analyze the static responses of laminated composite beam with partial shear interaction, a common structure in civil engineering, subjected to a combination of an arbitrary transverse load and a constant axial force. To account for the interfacial slip, a non-continuous model of slip stiffness along the interface was integrated into the SSA. Numerical results suggested that the non-uniformity of the slip stiffness significantly influences the critical axial load and interactions of the composite beam. Furthermore, Xu and Wu [17] developed a new plane stress model of partial interaction composite beam with interlayer slips based on the SSA and presented analytical solutions for static responses of simply-supported beams. It was found that the 2D model predicts deflections more accurately than the 1D theory, which neglects the shear deformation of the beam. Additionally, the rigidity of the shear connectors for partial interaction has a substantial effect on the flexural stiffness of composite beams. Subsequently, they conducted an analytical study of composite beams strengthened by externally and adhesively bonded reinforcements, such as fiber-reinforced polymer (FRP) or steel with variable cross-sectional properties [18]. The interfacial shear stress and axial force in external reinforcement were particularly investigated, and it was found that the bonded FRP with tapered ends and the ways of tapering the FRP significantly alter the magnitude and distribution of the shear stress at the interfaces. The developed method provided an efficient tool for analyses of the debonding problem and design of external reinforcement of composite beams. Ying et al. [15] applied the SSA to study static bending and free vibration of functionally graded material (FGM) beams resting on a Winkler-Pasternak elastic foundation based on 2D plane-stress theory of elasticity. They found that the gradient index, aspect ratio, and foundation parameter significantly influence the deformation and natural frequencies of such an FGM beam, and these exact solutions could serve as a benchmark for the future studies on FGM beams resting on elastic foundations.
FIGURE 2
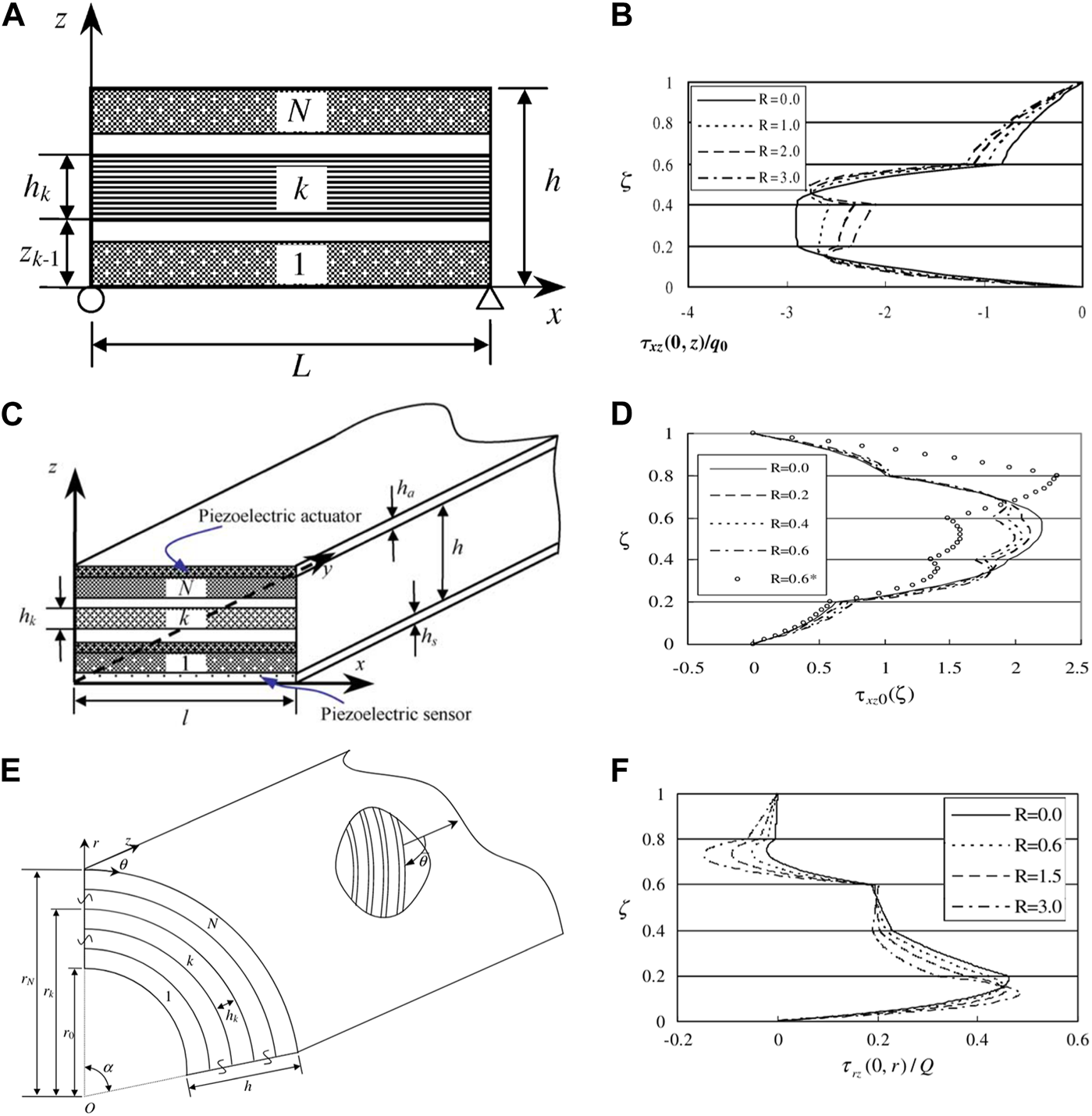
Laminated structures of beam, plate, and shell configurations and their shear stress field predicted by the 3D state-space approach: (A) laminated beam with bonding imperfection [14]; (B) the distribution of transverse shear stress of laminated beam in (A) along the thickness direction under different imperfect bonding parameter R; (C) imperfect laminated plate in cylindrical bending with surface piezoelectric layer [29]; (D) the distribution of transverse shear stress of laminated plate in (C) along the thickness direction under different imperfect bonding parameter R; (E) laminated cylindrical panel with bonding imperfection [60]; (F) the distribution of shear stress of laminated panel in (E) along the thickness direction under different imperfect bonding parameter R (Reproduced with permission from Chen et al. [14], copyright 2003 by AIAA; reproduced with permission from Chen et al. [29], copyright 2004 by Elsevier; reproduced with permission from Cai et al. [60], copyright 2004 by Elsevier).
Unlike conventional laminated structures composed of elastic materials, smart structures, which integrate host laminated structures with smart components such as piezoelectric actuators and sensors, can react to environmental changes through actuating, sensing, and control [78–80]. By utilizing the SSA and the LAT, Bian et al. [16] conducted an exact analysis of the static and dynamic responses of simply-supported FGM beams integrated with surface piezoelectric actuator and sensor. The influence of the bonding adhesives between the host beam and piezoelectric actuator and sensor layers on the displacements, stresses, and natural frequency was systematically examined. The results demonstrated that imperfect bonding reduces the global stiffness of the entire beam structure, as evidenced by the increase in deflection and the decrease in natural frequency. Yan et al. [19] explored the time-dependent responses of this smart structure with viscoelastic interfaces, described by the Kelvin-Voigt viscoelastic model, by using the SSA and power series expansion. They discovered that the viscoelastic interfaces also contribute to the reduction of the effective stiffness of the entire structure, and the developed method can be applied for damage analyses in health monitoring of aeronautical and engineering structures. Furthermore, Yan et al. [23] investigated the dynamic responses of a simply-supported laminated beam bonded or embedded with piezoelectric layers based on the SSA. The electromechanical impedance (EMI) technique was employed to monitor interfacial defects, described by a linear spring-like model, in the laminated beam. Numerical results revealed that the output electric signal is sensitive to the bonding condition between the piezoelectric layer and the host beam, suggesting that monitoring the EMI can be used to conveniently detect the interfacial defects. In addition, Alibeigloo [20] provided the analytical solutions for simply-supported FGM beams integrated with piezoelectric actuator and sensor under an external electric load and thermo-mechanical load, based on the state-space formulations and Fourier series expansion. They found that the effect of thermal load on mechanical behaviors is greater than that of mechanical load, and the effect of applied voltage is strongly dependent on the length-to-thickness ratio. Using the SSA and Fourier series expansion, Qian et al. [21, 22] proposed an exact analytical method to predict thermal responses of simply-supported and clamped laminated beams subjected to non-uniform temperature boundary conditions. For the clamped support, an equivalent model was introduced to convert the clamped support to a simple support. Numerical simulations indicated that the surface temperature, length-to-thickness ratio, material properties, and the layer number of laminated beam significantly affect the distributions of the temperature, displacements, and stresses. Moreover, the comparison of the results with those from the FEM verified the accuracy and effectiveness of the proposed method.
Laminated Plates
Compared to beam configuration, the mechanical behaviors of laminated plate structures have garnered more attention from researchers. Since 1969, a variety of exact solutions for laminated composite plates have been derived using Pagano’s approach [81–88]. However, this method necessitates the discussion of different eigenvalue cases to obtain the real solutions of the governing equations. In contrast to Pagano’s approach, the SSA offers a uniform matrix expression and serves as a powerful and efficient tool for exact analyses of laminated plates, given that the number of the undetermined constants is independent of the number of structural layers. This subsection summarizes the applications of 3D SSAs in the studies on the mechanical behaviors of laminated plates.
Fan and Ye [30] utilized the 3D theory of elasticity to derive the state equations of an orthotropic elastic body and then presented a series solution of a simply-supported rectangular plate under various mechanical loads. Their numerical results indicated significant deviations between existing plate theories, such as Reissner’s and Ambartsumyan’s theories, and their exact results. Subsequently, they presented exact solutions for the static and dynamic responses of three-ply orthotropic thick plates with simply-supported edges [24]. Numerical simulations demonstrated that the SSA surpasses the conventional displacement method of elasticity for laminated plates, as the latter increases the number of equations and unknown constants with the increase of the plies. They also established the state-space formulations for the exact analyses of the axisymmetric free vibrations of transversely isotropic three-ply circular plates with simply-supported and clamped edges [49]. Comparisons with the Reissner and Mindlin theories revealed the insufficient accuracy of the existing plate theories. Zenkour [31] introduced an exact and unified tool for the symmetric and antisymmetric analyses of rectangular laminated plates subjected to sinusoidally/uniformly distributed loads based on the SSA. The results were compared with those in Refs [82, 84], demonstrating the computational efficiency and accuracy of the SSA. Qing et al. [50] presented a new solution governed by the state-space formulations for the dynamic analyses of 3D elastic laminated plates with damping effect, using the precise integration method and Muller method. They examined the effects of damping parameters on natural frequency, harmonic vibration, and complex frequency response, which showed the predictive capability of their approach.
In contrast to the perfect bonding in the aforementioned works, Chen et al. [25] investigated the influence of interlaminar bonding imperfections, described by a linear spring layer model, on the bending and free vibration of a simply-supported cross-ply laminated rectangular plate using the SSA. Their numerical results were compared with those predicted by the plate theory developed in Cheng et al. [89], indicating that the approximate theory performs well for moderately thick laminates with perfect bonding, but is inaccurate for imperfect bonding. Chen et al. [32, 33] then use the SSA to analyze the bending of a simply-supported angle-ply laminated plate and a thick orthotropic laminate with viscous interfaces under static load, respectively. They found that the static response of the laminate is highly sensitive to the presence of viscous interfaces. They also investigated the cylindrical bending and free vibration of a simply-supported angle-ply laminate with interfacial damage, described by the general spring-layer model, using the SSA [26]. Numerical results suggested that the deformation and frequency’s sensitivity to interfacial damage could be used in nondestructive testing of structural damage. Qing et al. [34] used the SSA along with interfacial spring-layer model to study the energy release ratio of stiffened laminates with a planar delamination. They discussed the effect of the stiffeners on the distribution of the energy release modes, and the results revealed that their approach is a powerful and accurate alternative for solving the multiple delamination problems of laminated structures.
In addition to the previously mentioned studies on laminated plates composed of elastic materials, a series of theoretical research have been conducted on the mechanical behaviors of smart laminated plate structures. These structures combine host laminated plates with intelligent material layers to modify the structural responses through sensing, actuation, and control. For instance, Xu et al. [35] utilized the 3D SSA and Fourier series expansion to examine the coupled thermo-electro-elastic response of a smart laminated plate composed of fiber-reinforced cross-ply and piezo-thermo-elastic layers. They computed the sensitivity of the static response to variations in the mechanical, thermal, and piezoelectric material constants of the plate. Their results could serve as a benchmark for evaluating the accuracy and validity range of 2D models for such smart hybrid plates. Subsequently, they presented 3D analytical solutions for the free vibrations of laminated plates composed of the fiber-reinforced cross-ply and piezo-thermo-elastic layers, with initial stresses generated by either a temperature change or an electric load [51]. They obtained the frequency sensitivity to variations of various material constants and established a simple approximate formula for the sensitivity coefficients. This provided insight into the frequency dependence of initially stressed laminates on initial temperature, electric load, and geometric and material parameters. Lee and Jiang [36] first derived the state-space formulations for a 3D piezoelectric laminate of 6 mm material symmetry and performed an exact analysis of the coupled electroelastic behaviors of a simply-supported rectangular piezoelectric laminated plate subjected to a mechanical or electric load. The established state-space equations provided a useful means for the future studies on piezoelectric laminated plates with general interlayer (imperfect contact) or boundary conditions (bonded with foundations). Cheng and Batra [37] proposed an asymptotic expansion method to reduce the 3D equations to a hierarchy of 2D equations and used the SSA to investigate the deformations of multiple-electroded piezoelectric laminates subjected to surface tractions and surface and internal electric potentials. Numerical results showed excellent agreement with available exact solutions and demonstrated the errors of existing 2D piezoelectric plate models. Benjeddou and Deu [90] proposed a mixed SSA that retained the standard state displacement and transverse stress augmented with the electric potential and electric displacement to deal with the closed and open electric boundary condition. Its application to the exact analysis of transverse shear actuation and sensing of simply-supported three-layered plates with a piezoceramic core was then performed [38]. The influences of the plate aspect ratio, mechanical and electric excitation amplitudes, and the position and thickness of piezoceramic core on the static responses of the smart laminated plate were examined. The results were useful for comparison with approximate theories and numerical solutions. Vel and Batra [39] presented an exact 3D state-space solutions for the static cylindrical bending of simply-supported laminated plates embedded with shear mode piezoelectric actuators and subjected to mechanical and electric loads on the upper and lower surfaces. They then performed an exact analysis of the 3D deformations of such a smart laminated plate under mechanical and electric loads [40]. The exact displacement and stress solutions for different plate aspect ratios were compared with those obtained by the first-order shear deformation theory (FSDT). They found that the deviation between the FSDT and the exact solutions increases as the plate aspect ratio decreases. Additionally, Chen et al. [52] derived the state-space equations for free vibrations of transversely isotropic piezoelectric bodies, and numerical results illustrated that the results by 2D plate theory deviate from their exact solutions. Ding et al. [41] derived the axisymmetric state-space formulations of piezoelectric laminated circular plates based on 3D theory of piezoelectricity and the finite Hankle transform. They obtained the exact solutions for the rigidly-slipping support and elastically-simple support, which exhibited good agreements with those from the FEM. Following this, Ding et al. [53] established new state-space formulations with lower orders for transversely isotropic piezoelectricity by introducing two displacement functions and two stress functions. They then investigated the free vibration of a simply-supported rectangular piezoelectric laminated plate. The exact results obtained could serve as a benchmark for evaluating 2D approximate plate theories and numerical methods. Utilizing the Hankel transform, Wang [42] transformed the state-space formulation for the non-axisymmetric space problem of transversely isotropic piezoelectric media in cylindrical coordinate. They then presented the analytical solution of a semi-infinite piezoelectric medium based on the transfer matrix method. Subsequently, Wang et al. [43–45] similarly established the state-space formulations for axisymmetric problems of transversely isotropic piezoelectric media using the Hankel transform and transfer matrix method. Simulation results demonstrated that their novel approaches have higher computational efficiency than the classical displacement method and could be used to derive solutions for more complicated loads and boundary conditions. Qing et al. [54] established a state-space formulation for dynamic problems of simply-supported rectangular piezoelectric laminated plates, taking into consideration the transverse shear deformation and rotary inertia of laminate. This was based on the inversion of Laplace transform and modified mixed variational principle. Its application to the analysis of harmonic vibration and transient response of the laminate was presented to demonstrate its accuracy. The results can serve as benchmarks for testing thick plate theories and novel numerical methods. Using the SSA and recursive solution approach, Sheng et al. [46] presented an exact solution for thick orthotropic and piezoelectric laminated plates with clamped and electric open-circuited boundary conditions. The results, which agreed well with those of existing analytical solutions and finite element models, verified the effectiveness of the method. In contrast to the existing works on FGMs with a certain exponential law for the variations of physical fields along the thickness direction, Lezgy-Nazargah [47] performed an exact analysis of cylindrical bending of FGM piezoelectric laminates with arbitrary gradient compositions based on the SSA. The exact solutions, which exhibited excellent agreement with the published results, could be used to assess the accuracy of approximate plate theories and numerical methods.
In addition, Chen et al. [27–29] conducted a series of research on the effect of imperfect bonding on the mechanical behaviors of smart laminated plates, akin to previous research on composite laminates composed of elastic materials. Chen et al. [27, 28] developed 3D state-space formulations to investigate the bending and free vibration of simply-supported orthotropic and angle-ply piezoelectric rectangular laminates. These laminates had interlaminar bonding imperfections, which were modeled using a general spring layer. Concurrently, they explored the cylindrical bending and free vibration of simply-supported adaptive angle-ply laminates, which were bonded with surface piezoelectric actuator and sensor layers [29], as shown in Figure 2C. The interfaces between the host elastic laminate and piezoelectric layers were perfect, but the interlaminar bonding of the host laminate was imperfect. Figure 2D illustrated that the transverse shear stress predicted by 3D SSA is exactly continuous at interlayer interfaces for R = 0 and the imperfect bonding parameter R has a substantial effect on the distribution of shear stress field along the thickness direction. The precise solutions, grounded in 3D exact theories of elasticity and piezoelectricity, are instrumental in the development and validation of 2D approximate theories and numerical methods. Wang et al. [48] formulated state-space equations for 3D, orthotropic, and linearly magneto-electro-elastic media and investigated the static deformations of a simply-supported laminated rectangular plate under mechanical and electric load. The numerical results were compared with those by Pan [91] to validate the SSA. This approach could be extended for analyses of such smart composite plates with general interlayer and boundary conditions.
Laminated Shells
Shells represent a common class of contemporary structures, with laminated shells offering the benefits of light weight, high strength, and excellent design flexibility in structural configurations. These structures have been extensively employed in critical components across modern aeronautical, aerospace, and transportation industries, including aircraft cabins, radome, rocket adapter, satellite central cylinder, missile fairings, and more. The application of state-space technique in exact analyses of cylindrical shell structure was realized by Soldatos and Hadjigeorgiou [62, 63] using a proposed successive approximation method. They segmented the cylindrical shell into numerous successive and coaxial sub-shells and transformed the Navier-type governing equation of 3D linear elasticity into a set of simpler differential equations for thin shells, based on power series expansion. Subsequently, they derived the state equation and obtained the exact solutions for the free vibration of simply-support homogeneous isotropic cylindrical shells. As the layer number of sub-shells increases, the solutions based on successive approximate method converge towards the exact solutions to the free vibration problems of the shell structure. This successive approximation method paves the way for exact analyses of laminated shells using the SSA. This subsection reviews the relevant research on the static and dynamic responses of 3D laminated shells and panels based on SSAs.
Utilizing the successive approximation method, Hawkes and Soldatos [64] conducted an exact analysis of longitudinal vibrations of homogeneously orthotropic and cross-ply laminated hollow cylinders. Numerical results validated the efficiency and rapid convergence of this approach for addressing vibration responses in laminated shell structures. Soldatos and Ye [55] further examined 3D static, dynamic, thermoelastic, and buckling behaviors of simply-supported homogeneous and cross-ply laminated hollow cylinders and cylindrical panels using successive approximation method. In-depth studies of 3D flexural vibrations [65], stress and displacement distributions [61], and buckling behaviors [69] of laminated hollow cylinders and open cylindrical panels of symmetric and antisymmetric cross-ply were carried out by them. They used the successive approximation method in conjunction with transfer matrix method, which consistently resulted in the solutions of a sixth-order system of algebraic equations, irrespective of the layer number of the structures under consideration.
Fan and Zhang [58] derived the state equations for orthotropic and doubly curved shells and presented the analytical solutions for static and dynamic responses under simply-supported boundary conditions. This was based on the Cayley-Hamilton method and the SSA. Numerical results indicated that the method can be used to study laminated shell structures with arbitrary thickness. It also has the advantage that the scale of the final algebraic equations is independent of the layer number of the structure. Ding et al. [56, 57] performed the exact analyses of axisymmetric deformation, vibration, and buckling behaviors of simply-supported thick laminated closed cylindrical shells using the SSA. Simulation results demonstrated the efficiency and rapid convergence of this method. By introducing the Hellinger-Reissner variational principle and auxiliary function at the lateral boundary, Ding and Tang [66] employed this method to investigate the 3D free vibration of thick laminated cylindrical shells with two clamped edges. The results were in good agreement with those by the FEM, indicating the accuracy of the developed method for analyses of laminated shells with complex boundary conditions. Chen et al. [67] established the state-space formulations for generally anisotropic materials with thermal effect and carried out a 3D vibration analysis of fluid-filled orthotropic FGM cylindrical shells under simply-supported boundary conditions using the SSA. The effects of geometric sizes, material gradient index, and fluid contact on natural frequencies were examined. Numerical results revealed that the natural frequencies predicted by the SSA agree well with the exact solution in [92], validating the effectiveness and accuracy of the present method. Moreover, the fluid contact and the decrease of material gradient index lower natural frequencies, and these relationships are significantly dependent on the thickness of cylindrical shells. Chen et al. [59, 60] carried out the bending and vibration analyses of simply-supported cross-ply and angle-ply laminated cylindrical panels with weak interfaces as shown in Figure 2E, described by the spring-layer model, using the SSA in conjunction with the LAT. It was found that the imperfect bonding significantly influenced the distribution of the physical fields, such as the shear stresses in Figure 2F, along the thickness direction of laminated shell. Numerical comparison showed that the SSA along with the LAT can be used for the exact prediction of interface damage in laminated panels through natural frequencies in health diagnosis of structures. Moreover, the existing shell theories derived for perfect laminated structures were no longer suitable for effective analyses of laminated structures with imperfect interfaces. In addition, Talebitooti et al. [70] presented 3D analytical solutions for wave propagation in simply-supported orthotropic cylindrical shells with arbitrary thickness subjected to subsonic external flow pressure using the SSA along with the LAT. The sound transmission loss (TL) of a thick-walled cylindrical shell at oblique incidence was calculated. It was found that for thick-walled shells and the plane wave in high frequencies, the significant difference of the obtained TL from the 3D analytical method and conventional shell theories can be observed due to the shear and rotation effects. Thus, the 3D analytical solutions predicted by the developed method could be a benchmark for validating the approximate shell theories when modeling waves propagating in thick laminated shells.
In addition to the aforementioned cylindrical shell structures, laminated spherical shells have also found extensive applications in aerospace, structural engineering, and geophysics [93–96]. By introducing several displacement and stress functions, Chen and Ding [73] established the state-space formulations of spherically isotropic elastic body. Then they presented the exact solutions for static deformations of a three-layered spherical shell subjected to distributed uniform pressure. They further employed this method to study the free vibration of multi-layered spherically isotropic hollow spheres [75]. The frequencies of vibration modes of different orders obtained through this method are in good agreement with the results predicted by conventional 3D method. These results underscored the accuracy and effectiveness of the SSA, particularly when dealing with spherical shell structures with multiple layers. These exact solutions also serve as a benchmark for validating approximate shell theories and numerical methods. Similarly, by introducing displacement and stress functions, two separated state-space formulations of a spherically isotropic piezoelectric body were derived by Chen et al. [74]. They then performed an exact static analysis of a laminated, spherically isotropic, and piezoelectric hollow sphere. The results obtained are in excellent agreement with the exact solutions provided by Heyliger and Wu [97], indicating that the method offers an efficient and powerful tool for 3D exact analyses of laminated piezoelectric spherical shells. Subsequently, Chen et al. [76] employed this SSA to study the free vibrations of FGM piezoceramic hollow spheres with radial polarization, based on the LAT. They found that the piezoelectric effect and material gradient index have significant influences on natural frequencies. Furthermore, the SSA in conjunction with the LAT could be applied to the 3D exact analysis of arbitrary nonhomogeneous spherical shell structures.
In recent years, dielectric elastomers (DEs), characterized by their electromechanical coupling and large deformation capability, have garnered increasing interest from researchers. These materials are being explored for the development of soft, lightweight, and small-scale actuators, sensors, transducers, and soft robotics [98, 99]. Efforts have been made to study vibration and wave behaviors in nonhomogeneous or laminated DE shells using the state-of-the-art SSAs. For instance, Zhu et al. [68] utilized the SSA in conjunction with the LAT to conduct an exact analysis of axisymmetric torsional and longitudinal vibration in an incompressible DE cylindrical shell. The shell was subjected to axial pre-stretch and inhomogeneous electric biasing fields induced by the radial voltage. It was found that the natural frequencies of the DE cylindrical shells predicted by the SSA are in good agreement with those from the exact solutions for different axial mode numbers. Wu et al. [71] investigated the guided circumferential shear-horizontal (SH) -type and Lamb-type waves in an incompressible DE cylindrical shell subjected to inhomogeneous biasing fields based on the SSA along with the LAT. Numerical results demonstrated the accuracy and efficiency of the SSA for analyses of wave propagations in inhomogeneous shell structures. The study also found that the propagation properties of two types of guided circumferential waves are significantly dependent on the biasing fields and geometric sizes. Subsequently, they further employed this method to analyze the axisymmetric torsional and longitudinal waves propagating in an FGM DE cylindrical shell under the complex loads of axial pre-stretch, radial pressure, and radial electric voltage [72]. Simulation results indicated that the pre-stretch, radial pressure difference, and electric load can be utilized to steer the propagation behaviors (e.g., frequency and wave velocity) of the axisymmetric guided waves in the FGM DE cylindrical shells. The material gradient index has a significant influence on the tunable capacity of these external loads. Additionally, Mao et al. [77] performed the 3D torsional and spheroidal vibration analyses of an incompressible DE spherical shells subjected to inhomogeneous biasing field induced by radial electric voltage and radial pressure difference. This work was also based on the SSA in conjunction with the LAT. Numerical results illustrated that the SSA is also suitable for vibration prediction of DE spherical shells with high accuracy. Furthermore, it was found that the natural frequencies of various vibration modes in DE spherical shell can be flexibly tuned by adjusting the external electric voltage and internal pressure.
Simplified State-Space Approaches to Laminated Structures
Drawing upon structural theories such as beam, plate, and shell theories, a variety of simplified state-space formulations have been developed. These formulations, tailored to specific structural configuration, have been extensively utilized to investigate the mechanical behaviors of laminated structures based on the transfer matrix method. This section provides a comprehensive review of the evolution of these simplified SSAs with reduced dimensions. Furthermore, it highlights the progress made in the corresponding applications to the analyses of static and dynamic responses of laminated structures in beam, plate, and shell configurations. A summary of these developments is provided in Table 2.
TABLE 2
| Configuration | Structural theory | Mechanical behavior | Reference |
|---|---|---|---|
| Beam | CBT, FOBT HOBT | Static and dynamic responses | [100–102] |
| Beam | CBT, FOBT, HOBT | Dynamic response | [103, 104] |
| Beam | CBT, FOBT, HOBT | Static response | [105–109] |
| Beam | CBT | Dynamic response | [10, 110–113] |
| Beam | Zig-zag beam theory | Dynamic response | [114] |
| Beam | HOBT | Static response | [115, 116] |
| Beam | FOBT | Dynamic response | [117] |
| Plate | CPT, SDPT | Static and dynamic responses | [118] |
| Plate | CPT, SDPT | Static response | [119, 120] |
| Plate | YNS plate theory | Static response | [121] |
| Plate | SDPT | Static response | [122, 123] |
| Plate | SDPT | Static and dynamic responses | [124–130] |
| Plate | SDPT | Dynamic response | [131] |
| Plate | TVPT | Static response | [132] |
| Plate | FVPT | Static and dynamic responses | [133] |
| Plate | FVPT | Dynamic response | [134] |
| C-shell | CST, FOST, TOST | Static and dynamic responses | [135] |
| C- and S-shells | CST, FOST, TOST | Static and dynamic responses | [136] |
| C- and S-shells | CST, FOST, TOST | Dynamic response | [137] |
| C-shell | FOST | Dynamic response | [138, 139] |
Summary of simplified state-space approaches based on structural theories and their applications in the mechanical analyses of complex structures in beam, plate, and shell configurations.
Acronyms: CBT, classical beam theory; FOBT, first-order beam theory; TOBT, third-order beam theory; CPT, classical plate theory; SDPT, shear-deformation plate theory; YNS, Yang, Norris, and Stavsky; TVPT, two-variable plate theory; FVPT, four-variable plate theory; CST, classical shell theory; FOST, first-order shell theory; TOST, third-order shell theory; C-shell, Cylindrical shell; S-shell, spherical shell.
Laminated Beams
As early in 1950, Thomson [10] pioneered the establishment of state-space formulations for the depiction of beam bending, utilizing the simplified beam theory. This was followed by a free vibration analysis of a non-uniform beam, employing the LAT and transfer matrix method. After nearly four decades of gradual development, the SSAs have regained significant attention from the research community, spurred by the rapid emergence and widespread application of laminated composite structures.
Khdeir and Reddy [100, 101] presented analytical solutions for the buckling and free vibration of cross-ply laminated beam with arbitrary boundary conditions. These solutions were derived using the SSA in conjunction with the refined beam theories. Numerical results revealed that the discrepancies among different shear deformation theories are significantly less than that between any of them and the Euler-Bernoulli beam theory. Moreover, as the length-to-thickness ratio increased, the difference in critical buckling loads and natural frequencies between shear deformation theories and Euler-Bernoulli theory diminishes. Subsequently, Khdeir [103] presented an analytical solution for the transient response of antisymmetric cross-ply laminated beams with generalized boundary conditions and under arbitrary loads. This was achieved by using the classical, first-, and third-order shear deformation beam theories in tandem with the SSA. The study concluded that the results predicted by the high-order theory of Reddy (HOBT) and Timoshenko shear deformation beam theory are more accurate than those predicted by the Euler-Bernoulli theory for thick beams. Furthermore, Khdeir and Reddy [105] developed the analytical solutions for the bending of symmetric and antisymmetric cross-ply laminated beams with arbitrary boundary conditions and subjected to arbitrary loads. They found that the shear deformation, orthotropic ratio, symmetry of cross-ply, and boundary conditions significantly influence the deflection of laminated beams. They also employed this method to analyze the thermoelastic response of symmetric and antisymmetric cross-ply laminated beam under arbitrary boundary conditions and subjected to general temperature fields [106]. The study concluded that the effect of temperature fields on the deflection of composite beam is significantly dependent on layer number, shear deformation, cross-ply symmetry, and boundary conditions. The thermal buckling of cross-ply laminated beams subjected to uniform temperature distribution was also investigated by them [107] using the refined beam theories in conjunction with the SSA. The effects of length-to-thickness ratio, modulus ratio, thermal expansion coefficients, boundary conditions, and layer number on the critical buckling temperature were systematically discussed. In addition, Srinivasan et al. [115] developed a unified SSA based on different HOBTs taking both normal strains and shear deformation effects into consideration. They then presented analytical solutions for laminated composite beams subjected to transverse loads and under various boundary conditions. In the four HOBTs, shear deformation was described by four warping functions corresponding to exponential, hyperbolic, trigonometric, and parabolic functions. Comparative studies revealed that the models associated with the exponential and hyperbolic functions yield accurate and identical results in all studies. Ramaprasad et al. [116] established a unified state-space coupled field formulation for generating analytical solutions for thin-walled composite open section beams, which are extensively used in aerospace. All non-classical effects such as torsional warping, warping shear, material coupling, and shear deformation were taken into consideration. The results for arbitrarily laminated non-symmetric composite channel and I-section beams subjected to bending and torsional loads showed excellent agreement with the reported results in Ref. [140], validating the efficiency and accuracy of the proposed method.
Considerable research has been conducted to investigate the mechanical behaviors of smart beam systems, utilizing simplified beam theories and the SSA. For instance, Pota and Alberts [110], building on the Euler-Bernoulli beam theory, developed an SSA for the free vibration analysis of a slewing beam system. This system was bonded with piezoelectric sensors and actuators, which were applied by an external voltage. For the special case where the hinged end of the structure was clamped, the results obtained agree with those presented in Ref. [141]. Based on the first-order beam theory (FOBT) and HOBT, Aldraihem and Khdeir [108] presented analytical solutions for the bending of beams bonded with thickness-shear and extension piezoelectric actuators under various boundary conditions using the SSA. They found that the operation modes of the piezoelectric actuator could result in significant difference between the deflections predicted from the FOBT and HOBT. Built upon the zig-zag beam theory in conjunction with the SSA, they also presented analytical solutions for the free vibration of soft-core sandwich beams with arbitrary boundary conditions [114]. The obtained results indicated that the support conditions have significant influences on the relationship between resonant frequency and length-to-thickness ratio. The comparison between the obtained results and the existing experimental, analytical, and numerical results in the literature showed that the zig-zag beam model provides accurate natural frequencies for sandwich beam with a soft core. These results also serve as useful benchmarks for approximate solutions from numerical methods like Rayleigh-Ritz method, FEM, etc. Furthermore, based on the Euler-Bernoulli beam theory, Palmeri and Adhikari [111] developed a Galerkin-type SSA for the transverse vibrations of slender double-beam system with a viscoelastic inner layer, described by standard linear solid model. Numerical results demonstrated the validity and accuracy of the proposed method in both frequency- and time-domain analyses. Subsequently, using this Galerkin-type analytical model, Palmeri and Ntotsios [112] investigated transverse vibrations of viscoelastic sandwich beams under different boundary conditions as shown in Figure 3A. It was found that the viscoelasticity significantly affect the frequencies and transverse mode shapes of the sandwich beams (see Figures 3B, C), and the numerical results verified the accuracy and versatility of the proposed method. Li et al. [113] also proposed a novel SSA for the transverse vibration analysis of a double-beam system. They introduced a mode-shape constant to the state space in the modeling framework to improve the computational accuracy and efficiency. Moreover, Sahmani and Ansari [109] investigated the buckling behaviors of nanobeams under various boundary conditions by utilizing nonlocal continuum beam models of different beam theories, including the CBT, FOBT, and Levinson beam theory (LBT), in conjunction with the SSA. The results obtained from the developed nonlocal beam model match those from the molecular dynamic simulation given by Ansari et al. [142], helping to predict the appropriate value of nonlocal parameter. It was also found that the nonlocal beam model and boundary conditions significantly influence the predicted value of nonlocal parameters. Additionally, Fazeli et al. [117] performed free and forced vibration analyses of smart orthotropic cross-ply laminated stepped beams integrated with a piezoelectric actuator, using the SSA based on the FOBT. The obtained natural frequency for piezoelectric sinusoidal excitation was compared with those from FEM and experimental study. It was found that the analytical method provides an efficient tool to predict the vibration behaviors of smart stepped laminated beam with high accuracy.
FIGURE 3
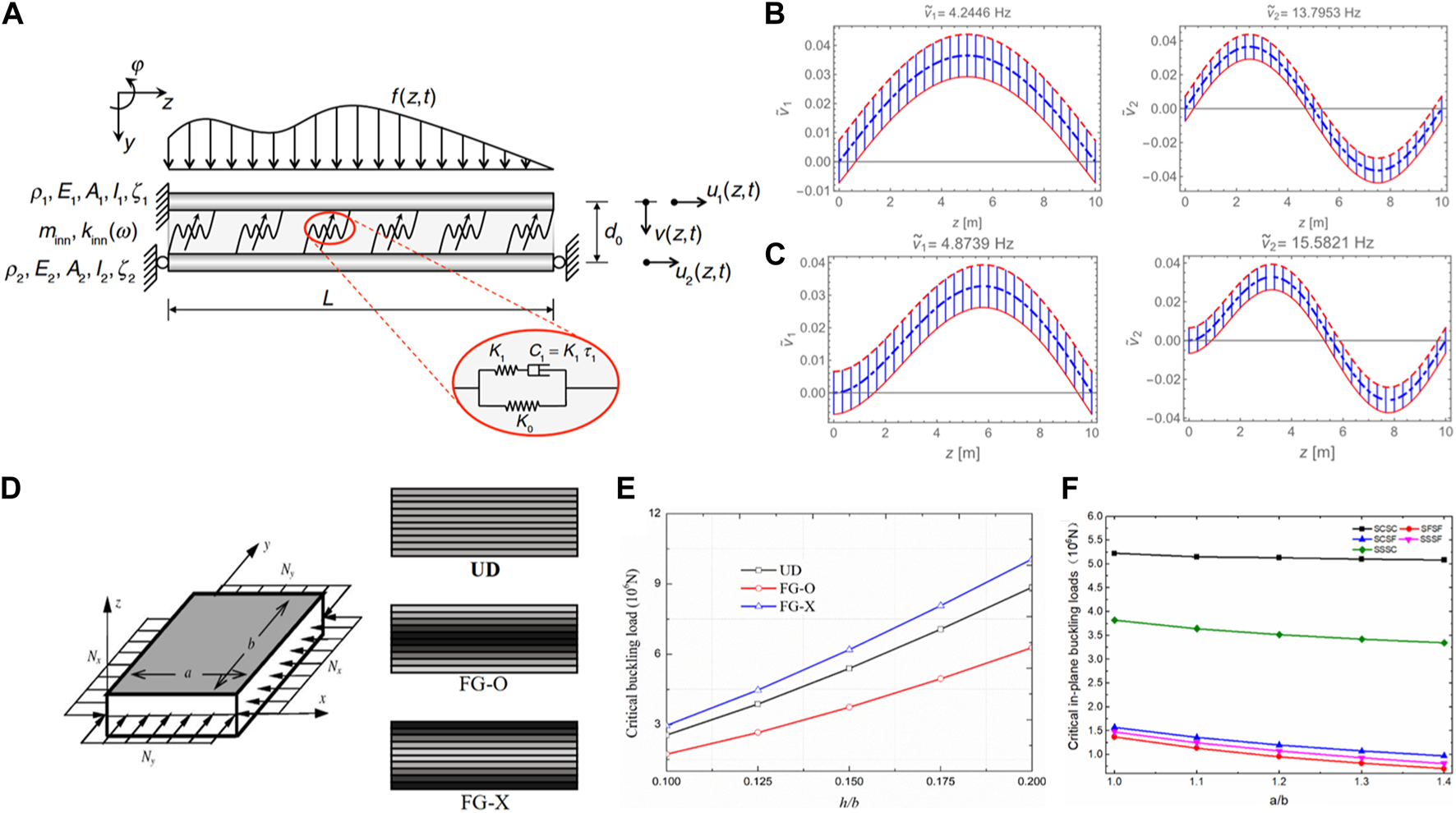
Laminated structures of beam and plate configurations and the mechanical responses predicted by the simplified state-space approaches: (A) viscoelastic sandwich beams with its viscoelastic core modeled by an elastic spring in series with a viscous dashpot [112]; (B) first two transverse modes for undamped sandwich beam; (C) first two transverse modes for damped sandwich beam; (D) graphene reinforced composite functionally graded material plate with different gradient distributions along thickness direction [131]; (E) variations of critical buckling loads versus thickness-to-length ratio; (F) effect of the width-to-length ratio on critical in-plane buckling loads under different boundary conditions for FG-X pattern (Reproduced with permission from Palmeri et al. [112], copyright 2016 by ASCE, Open Access; Reproduced with permission from Lv et al. [131], copyright 2019 by IOP Publishing, Open Access).
This paragraph highlights the recent work on applications of the SSA to the mechanical analyses of FGM laminated beams. Based on the CBT, FOBT, and HOBT, Trinh et al. [104] developed analytical solutions for predicting the fundamental frequency of FGM sandwich beams under various boundary conditions using the SSA. Simulation results revealed that boundary conditions, material parameters, layer arrangement, and length-to-thickness ratio all significantly affect the fundamental frequency of such an FGM sandwich beam. Subsequently, they presented analytical solutions for the buckling and free vibration of FGM beams under mechanical and thermal loads using the SSA based on the HOBT [102]. The results demonstrated the efficiency and effectiveness of the analytical model. By utilizing the multi-term Kantorovich-Galerkin method for describing the displacement components, Wang et al. [143] proposed a 2D elasticity model in conjunction with the SSA to investigate the bending and free vibration of laminated graphene-reinforced composite (GPC) beams. Five different graphene distribution patterns were presented by altering the volume fraction of graphene in each layer. The study found that the laminated GPC beam with pattern X exhibits the smallest deflection and highest fundamental frequency for a high length-to-thickness ratio. Conversely, it displays the largest deflection and smallest fundamental frequency for a low aspect ratio due to the decrease in the transverse shear stiffness.
Laminated Plates
Chandrashekara and Santhosh [144] pioneered the SSA for the free vibration analysis of cross-ply laminated plates, utilizing the Maclaurin series expansion along the thickness direction. The efficacy of this method was substantiated by comparing it with the exact elasticity solution for plates under the plane strain assumption. Their findings revealed that the SSA, even with a limited number of series expansion terms, yields results in excellent concordance with the exact results for both thin and thick plates. In a similar vein, the research team of Khdeir and Reddy carried out extensive studies on the development of SSAs based on approximate plate theories, demonstrating their applicability to the analyses of mechanical behaviors of laminated plates. For instance, Khdeir [124, 125] utilized the SSA to formulate Lévy-type solutions for the buckling and free vibrations of antisymmetric angle-ply laminated plates, based on the first-order shear deformation plate theory (FSDPT). Moreover, Khdeir and Reddy [119] generated Lévy-type solutions for the bending of antisymmetric cross-ply rectangular laminates under sinusoidal transverse loads, employing the classical plate theory (CPT), FSDPT, and third-order shear deformation plate theory (TSDPT) in conjunction with the SSA. Their numerical results highlighted significant discrepancies between the deflections predicted by the CPT and those from FSDPT and TSDPT under various boundary conditions. In another study, Khdeir [120] presented Lévy-type solutions for shear deformable antisymmetric angle-ply laminated plates, using the Yang, Norris, and Stavsky (YNS) theory in combination with the SSA. A comparative analysis between the Lévy-type solutions derived from the FSDPT and classical Kirchhoff plate theory in conjunction with the SSA [120] revealed significant difference between the results from the Kirchhoff plate theory and those from the FSDPT. In contrast to laminates with antisymmetric angle-plies, Librescu and Khdeir [122] proposed a higher-order plate theory and examined the static deformation of symmetric cross-ply laminated plates using the SSA. They further employed this method to investigate the buckling and free vibration of the same laminated plate under various boundary conditions [126]. Built upon the laminated anisotropic plate theory as considered in Refs [145, 146], Khdeir [127] generated Lévy-type solutions for the buckling and free vibration of symmetric cross-ply laminated plate utilizing the state-space technique. Khdeir [128] also used the SSA to develop the Lévy-type solutions for the buckling and free vibration of unsymmetric cross-ply laminated plates based on the refined shear deformation theory used in [147]. In [118], Khdeir commented on the application of the SSAs to bending, buckling, and free vibration analyses of composite laminates. It was concluded that for plate structures with the characteristic length-to-thickness ratio greater than 20, the results from [119–122, 124–126], [127, 128] obtained from different plate theories under various boundary conditions agree well with the exact solutions. Lastly, based on the FSDPT, Xing and Xiang [123] proposed an analytical method for the buckling of symmetric cross-ply composite laminates, using the separation-of-variable method in conjunction with the SSA to enhance the computational efficiency and circumvent numerically ill-conditioned problems. The accuracy and effectiveness of the analytical model were validated by comparing the numerical results with the those in the literature [126, 148].
SSAs have also been utilized to investigate the size-dependent behaviors of nanoplates. Leveraging the two-variable plate theory (TVPT) in conjunction with the Eringen’s nonlocal elasticity theory, Sobhy [132] examined the effect of hygrothermal conditions on the bending of orthotropic nanoplate under various boundary conditions. The study concluded that the results predicted by the TVPT agree well with the published solutions, suggesting that the TVPT is more accurate than the CPT. Furthermore, the deflection of the nanoplate was found to be directly proportional to the temperature, moisture concentration, scale parameter, side-to-thickness ratio, and modulus ratio, while inversely proportional to the length-to-thickness ratio and mechanical load. Trinh et al. [129] developed the state-space Lévy solutions for size-dependent static, free vibration, and buckling behaviors of FGM sandwich plates under diverse boundary conditions. The analysis was based on a refined shear deformation theory in conjunction with the modified couple stress theory. It was revealed that the material distribution, geometric parameter, characteristic length parameter, and boundary conditions significantly alter the deflections, stresses, natural frequencies, and critical buckling loads of the sandwich plate. The results obtained provide a valuable benchmark for mechanical analyses of FGM microplates. In a similar vein, several research groups have focused on the mechanical behaviors of FGM plates. For instance, Zhang et al. [130] employed the state-space Lévy method to investigate the vibration and buckling behaviors of functionally graded carbon nanotube (FG-CNT) reinforced composite rectangular plate subjected to in-plane loads, based on the TSDPT. The simulation results indicated that the CNT distribution, length-to-thickness ratio, and boundary conditions have substantial influences on the natural frequencies, mode shapes, and critical buckling loads of the FG-CNT composite plates. Additionally, Lv et al. [131] employed this theory to explore the vibration characteristics of moderately thick FGM graphene reinforced composite plates with different gradient distributions in Figure 3D under different boundary conditions. The effects of graphene distribution, plate thickness-to-width ratio, length-to-width ratio, and external load on natural frequency and critical buckling loads were thoroughly examined and discussed. Figure 3E showed that the dependence of critical buckling load on thickness-to-length ratio is affected by the gradient distributions of the graphene. Figure 3F revealed that the relationship between the critical in-plane buckling loads and the width-to-length ratio is dependent on the support conditions of the FGM plate. Utilizing the four-variable plate theory (FVPT) in conjunction with the SSA, Demirhan and Taskin [133] investigated the bending and free vibration of porous FGM plate with two opposite simply-supported edges. The influence of porosity parameter, plate aspect ratio, material gradient index on the deflections and natural frequencies were scrutinized. The analytical method was validated by comparing the obtained results with those in the literature [149]. Similarly, Rouzegar et al. [134] presented the state-space Lévy solutions for the free vibration of a smart laminated plate, with its FGM core sandwiched by two piezoelectric layers, based on the FVPT. A comparison between the results and those available in Refs [150, 151] verified the accuracy of the analytical model. It was concluded that the piezoelectric layer thickness, material graded index, plate geometric parameter, and boundary conditions significantly influence the natural frequencies of the smart composite structure.
Laminated Shells
Recent years have seen a surge in research focused on the development of simplified state-space formulations based on various shell theories and their subsequent applications in the mechanical analyses of laminated shells. Built upon the classical, first-order, and third-order shell theories, Khdeir et al. [135] developed analytical solutions for the bending, free vibration, and buckling behaviors of cross-ply circular cylindrical shells under various boundary conditions, utilizing the stat-space technique. The study explored the effects of boundary conditions, layer number, and shear deformation on the deflection, natural frequencies, and critical buckling loads. Numerical results indicated a significant deviation between the results from the classical shell theory (CST) and those form the shear deformation theories. Furthermore, the inclusion of transverse shear strain results in the discrepancies between results from the first-order shell theory (FOST) and third-order shell theory (TOST). Subsequently, Khdeir and Reddy [136] presented Lévy-type solutions for the bending, free vibration, and buckling of doubly curved cylindrical and spherical shells under various boundary conditions. These solutions were based on three types of shell theories in conjunction with the SSA, and the conclusions drawn were similar to those in Ref. [135]. In a related study, Ye and Soldatos [69] established the state-space formulations for the buckling analysis of simply-supported laminated hollow cylinders and cylindrical panels subjected to the single or combined mechanical loads, by neglecting the initial shear stresses. Simulation results showed that the trends of the critical buckling load parameter as a function of the stiffness of the hollow cylinder or cylindrical shell agree with the 3D exact results. The SSA exhibits higher efficiency than the FEM for the shell structures with a large number of layers. Recently, Dozio [137] developed general state-space Lévy-type solutions for the free vibration of orthotropic multilayered cylindrical and spherical panels under different boundary conditions. Various shell theories can be integrated according to the shell thickness, the degree of anisotropy of the considered problems, and the desired accuracy. Compared with the existing Lévy-type vibration solutions [152, 153], the final matrix of the present solutions was invariant with respect to the 2D kinematic shell theories. A single-layer spherical shell was selected as a numerical example and the comparison of the displacement fields obtained from the 2D shell theory and 3D theory validated the accuracy of the method for the single-layered spherical shell. Moreover, the accuracy of the developed 2D analytical model for multilayered shells strongly depends on the refinement of the 2D shell theory, especially when the panel is thick and exhibits strong material anisotropy. Hosseini-Hashemi et al. [138] performed a free vibration analysis of FGM viscoelastic cylindrical panel made of polymeric foams using the SSA, based on the FOST. The effects of geometric and material parameters as well as boundary conditions on natural frequencies were examined. The agreement of the obtained results with those from the FEM verified the validity and accuracy of the developed method. Finally, Razgordanisharahi et al. [139] employed the SSA to investigate the free vibrations of a honeycomb sandwich panel consisting of a hexagonal honeycomb core layer and two face sheets, based on the FOST. The comparison of the obtained results with those in previous studies verified the accuracy of the model. The simulation results revealed that the natural frequencies of the sandwich panel are also significantly dependent on the geometric parameters of the honeycomb core.
State-Space Approaches to Complex Periodic Structures
In addition to the previously discussed laminated structures in beam, plate, and shell forms, complex periodic structures, composed of numerous identical units or periodic arrays in varying geometric configurations, have been extensively utilized in various fields such as aerospace, civil and structural engineering, and marine. These applications include, but are not limited to, space antenna, aircraft fuselages, and ship hulls. The multitude of potential unit configurations or unit array often complicates the mechanical analyses of these complex structures. To mitigate this complexity, units of different configurations are often modeled using approximate structural theories, which can lead to significant discrepancies in predicting the mechanical behaviors of entire structures [154]. The FEM is frequently employed as a robust and effective tool for analyzing these complex periodic structures due to its vast and comprehensive library of elements. However, the natural frequencies of complex periodic structures composed of many identical units are typically closely grouped within frequency bands. The number of natural frequencies within each band is equal to the number of the repeated units in the structure [155, 156]. Consequently, accurately predicting the natural frequencies and corresponding mode shapes of these structures using the FEM can be both time-consuming and potentially inaccurate. To address these challenges, mixed transfer matrix methods (also called mixed SSAs) have been proposed that combine numerical or theoretical methods with the transfer matrix method based on state-space formulations. These hybrid approaches are particularly useful for handling the mechanical problems associated with complex periodic structures that have intricate unit configurations. This section will review the development and application of these mixed SSAs in the dynamic responses of these complex periodic structures, as summarized in Table 3.
TABLE 3
| Unit configuration | Method | Dynamic response | Reference |
|---|---|---|---|
| Beam | TMM | Vibration | [157–160] |
| Beam | TMM and WPA | Vibration | [161] |
| Beam | FEM and TMM | Wave | [162] |
| Duct, rod, and beam | TMM and SM | Wave and vibration | [163] |
| Beam | TMM and WPA | Wave | [164–166] |
| Beam | TMM and WPA | Vibration | [167, 168] |
| Pipe, beam, and truss | TMM and WPA | Wave | [169] |
| Beam and truss | FEM, TMM, and WPA | Wave | [170] |
| Truss | FEM, TMM, and WPA | Vibration | [171–174] |
| Truss | FEM, TMM, and WPA | Wave | [175] |
Summary of mixed state-space approaches and their applications in complex periodic structures composed of different unit configurations.
Acronyms: TMM, transfer matrix method; FEM, finite element method; WPA, wave propagation approach; SM, Spectral method.
Beam-Type Periodic Structures
Professor Y. K. Lin and co-workers have conducted extensive research on the dynamic behaviors of complex periodic beam structures on various flexible supports, utilizing the transfer matrix method based on state-space formulations. For instance, Lin and Mcdaniel [157] developed an analytical method for predicting the frequency response of a finite periodic Euler-Bernoulli beam on multiple elastic supports as shown in Figure 4A, which was seen as a simplified version of a skin-stringer panel system used in flight vehicle design [176], based on the transfer matrix method. They presented the frequency-response functions for both undamped and damped systems and discussed the effect of the dampers, modeled by spring-suspended mass, on frequency responses. Subsequently, Vaicaitis et al. [158] investigated the spatial decay in the dynamic response of an infinite damped periodic Euler-Bernoulli beam structure, supported by identical elastic springs and subjected to sinusoidal excitations at a specific unit. They discovered that the distance of spatial decay in frequency response is dependent on the excitation frequency, the shape of spectral density, and the cross-spectral density of the forcing field. They also found that dampers can be used for vibration control of such a periodic beam structure. Furthermore, Vaicaitis and Lin [161] analyzed the frequency response of a finite N-span periodic Euler-Bernoulli beam on evenly spaced elastic supports, subjected to turbulent boundary-layer pressure excitation. They used the transfer matrix method in conjunction with the flexural wave propagation approach. Numerical results demonstrated the convenience and suitability of the transfer matrix method based on state-space formulations in studying the dynamic response of periodic structures subjected to random pressure fields. Lin and Yang [159] carried out a free vibration analysis of a simply-supported disordered periodic beam using the transfer matrix method for state vectors. They considered two types of disorder: the random deviation of unit length from an ideal identical value and the random fluctuation of the bending stiffness. They revealed that random unit lengths significantly influence natural frequencies of different orders, but the effect of random bending stiffness on frequencies is negligible for such a disordered multispan beam. Moreover, random unit lengths also led to variability in the normal modes. Yang and Lin [160] further examined the effect of random unit-length deviations of a disordered periodic beam on multiple hinge supports on its frequency responses. They applied two types of excitations to the beam structure, namely, a concentrated force or moment and a distributed frozen force. Their numerical results showed that considering the disorder in unit lengths decreases the amplitude of the statistical average of the frequency response function, particularly near the resonance frequencies, but increases its standard deviation when approaching these frequencies. Furthermore, some vibration modes that do not appear in the frequency spectrum of a perfect periodic beam can be actuated in this disordered structure. Later, Yeh and Chen [162] employed the finite element method and transfer matrix method to analyze the longitudinal wave propagating in a periodic sandwich beam structure, where the base beam was covered by the constrained layer and viscoelastic layer. The study revealed that the length ratio and base beam materials could be used to tune the location and width of the stop and pass bands of this periodic structure, thereby filtering certain bands of frequencies. Assis et al. [163] examined the complex band structures and forced response of a one-dimensional phononic system with arbitrary geometric and material profiles using the transfer matrix method. They derived the transfer matrix of the system from a new spectral approach based on a Riccati differential equation with the impedance as variable. They explored phononic systems in duct, rod, and beam configurations, and the obtained results are consistent with those from traditional plane wave expansion method and spectral element method, thus validating the high accuracy and efficient computational cost of the method.
FIGURE 4
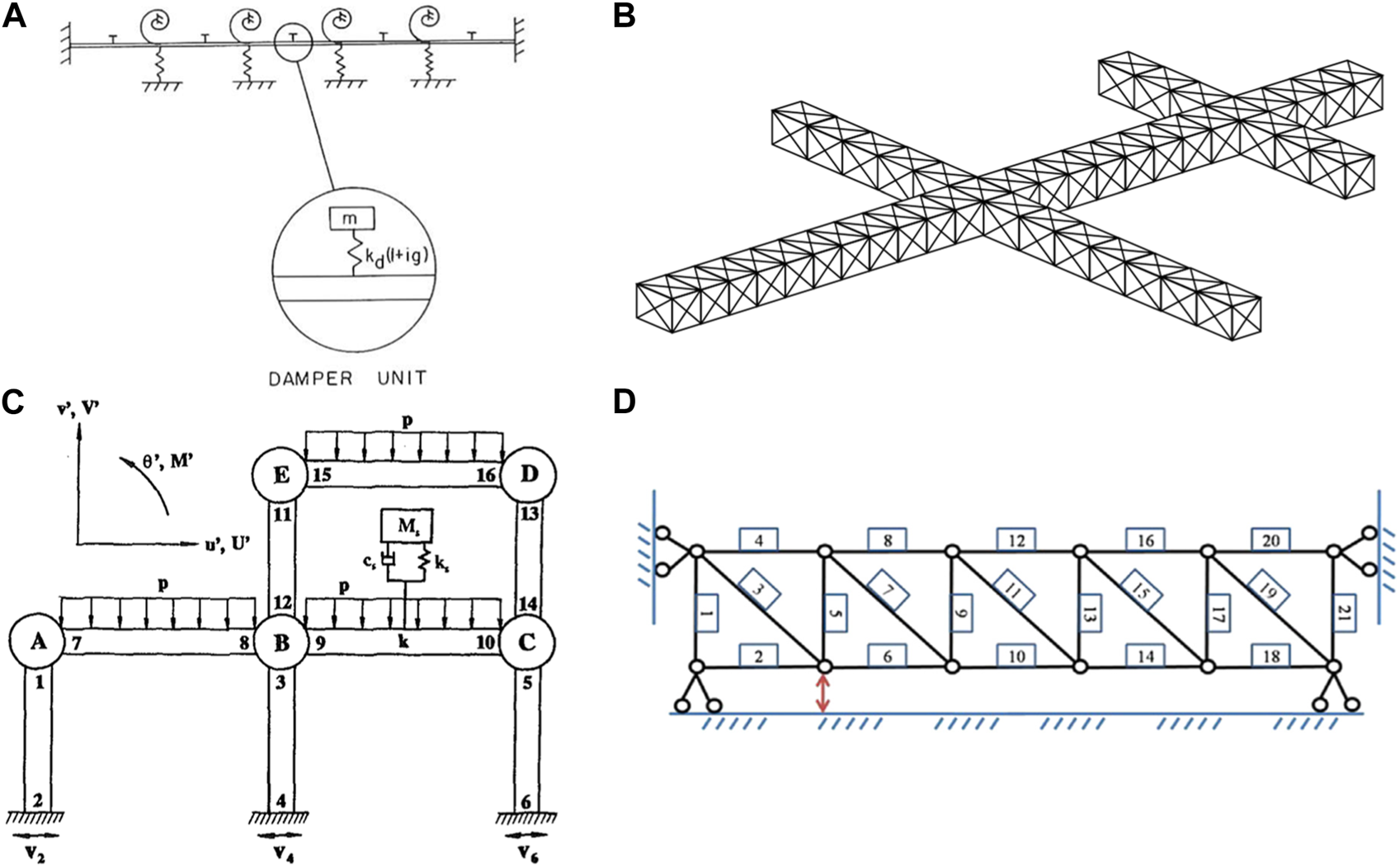
Some cases of periodic complex structures. (A) Periodic beam structure with periodic elastic supports [157]; (B) schematic of truss-type space periodic structure; (C) frame structure based on beams [175]; (D) small-scale five-span planar truss-type structure [174] (Reproduced with permission from Lin and Mcdaniel [157], copyright 1969 by ASME; reproduced with permission from Cai and Lin [175], copyright 1991 by ASCE; reproduced with permission from Ren and Zhou [174], copyright 2014 by Elsevier, Open Access).
In addition to the previously mentioned transfer matrix method, a wave propagation approach has also been adopted to investigate the dynamic behaviors of infinite or semi-infinite periodic structures. While this method falls outside the purview of this article, we provide a selection of representative literature [177–184] for the readers’ convenience. By integrating the transfer matrix method and wave propagation approach, Lin and others proposed an innovative theoretical method to analyze the dynamic response of long periodic beams subjected to external excitations. For instance, Lin et al. [164] investigated the dynamic behaviors of a surface-mounted pipeline, modeled as an infinitely long Euler-Bernoulli beam, under seismic excitation. The seismic input was introduced to the pipeline structure through evenly spaced supports. Simulation results validated the efficacy of this method, which could be expended to examine the effect of random variation of the support spacings and the ground motion on the pipeline’s response. Furthermore, Cai and Lin [165] explored the localization property of wave propagation in disordered periodic structures using the transfer matrix method in conjunction with the wave propagation approach. They proposed a new perturbation scheme to calculate the localization factor, defined as the average exponential decay ratio of wave propagation along the propagation direction, based on probability theory. The numerical example of a multi-supported Euler-Bernoulli beam with an additional torsional spring at each support highlighted two significant features of the developed method: its high accuracy and the inclusion of damping effect in practical structures. Moreover, they utilized the proposed method to study the high-level dynamic response near the point of dynamic excitation, induced by the structural disorder in a disordered periodic structure [167]. Their simulation results indicated that both the number of disordered units and the deviation level of disorder significantly influence the concentrated response near the excitation point. An increase in either one of these factors leads to larger standard deviations of responses. However, structural damping can help to reduce the response level and the likelihood for the responses to reach a much higher level. Additionally, Qiu and Lin [166] computed the localization factor of mono- and multi-channel waves in disordered periodic beam structures supported by linear torsional and translational springs. Their study found that the computed results agree well with those from Monte Carlo simulations, except near boundaries of each wave-passage band. Prof. Lin provided an insightful review of these works on wave propagation and frequency responses of disordered periodic beam structures [185]. Furthermore, Romeo and Paolone [169] employed the transfer matrix method to conduct the wave propagation analysis in three-coupled periodic structures among transversal, longitudinal, and torsional waves. They considered three types of periodic structures, namely, pipes, thin-walled beams, and truss beams. Their unique band structures, including the stop, pass, and complex domains, were computed and presented. Saeed and Vestroni [168] presented an exact closed-form method for frequency response analysis of periodic beam system under multiple excitations using the wave transfer matrix method. The wave solutions were formed by a free wave field incorporating the dynamic response of the entire structure and a forced wave field generated by constrained forces or external excitations. Two numerical examples, namely, a multi-constrained translating string and a beam on multiple supports, demonstrated the efficiency and accuracy of the proposed approach.
Truss-Type Periodic Structures
Complex truss-type structures composed of spatially periodic truss units are a prevalent form of large space structures as shown in Figure 4B used in aerospace and civil engineering due to their light weight, high strength, and design flexibility. The truss units are interconnected end-to-end, forming sections of a spatially periodic array, with different sections potentially intersecting or interconnecting. The dynamic analysis of these truss-type periodic structures presents a greater challenge compared to finite periodic beams for two primary reasons. First, the shared degrees of freedom at the interface between two adjacent truss units are larger than those between beam units. Second, the quantity of truss units surpasses that of beam units, and truss-type periodic structures are often considered infinitely long. To address these challenges, Lin and others proposed a novel method that integrates the FEM, the transfer matrix method, and the wave propagation approach. The FEM was employed to model a truss unit or each type of periodic unit array in the structure, accurately representing the dynamic characteristics of the unit, irrespective of its complexity. Traditional transfer matrices for state vectors were converted into the transfer matrix for wave vectors, enabling the identification of various types of waves, dependent on the number of degrees of freedom at the interface of two adjacent truss units, propagating along the structure in two opposite directions [186]. Moreover, the innovative concept of wave reflection and transmission matrices was introduced to replace single wave reflection matrix in the traditional wave propagation approach. This innovation circumvents computational errors associated with the apparent growing wave in the opposite propagation direction caused by the damping effect of practical structures.
Yong and Lin [170] applied this method to investigate the dynamic responses of long and complex periodic structures composed of beam and truss units under external excitation. Their numerical examples demonstrated that this method is more computationally efficient than applying the FEM directly to the entire structure. They [171] further studied the dynamic behaviors of complex truss-type periodic structures, consisting of two intersecting arrays of truss-cell units, subjected to sinusoidal and impulse point excitations. The numerical results validated the efficiency, accuracy, and numerical robustness of this novel method for analyzing truss-type space structures with damping. Built upon this method, Cai and Lin [175] performed the dynamic response analysis of engineering frame structures composed of interconnected slender components as shown in Figure 4C, subjected to either concentrated or distributed loads. Every slender component was treated as a multi-channel waveguide, with its dynamic property characterized by wave-reflection and transmission matrices. The entire frame structure was then conceptualized by a network of these waveguides. Numerical examples, encompassing different boundary types and external loads, demonstrated numerical efficiency and theoretical accuracy of this approach for analyzing frame structures composed of interconnected members. In a further development, Yong and Lin [172] developed an enhanced computational scheme for dynamic response analysis of truss-type space periodic structures with complicated structural configurations and subjected to arbitrary excitations. This scheme featured three significant improvements: the characterization of individual truss-arrays via wave-scattering matrices, a new bookkeeping system to track transmitted, reflected, and re-directed waves in various direction, and a procedure to eliminate step-by-step superfluous unknowns for simplifying the calculation. Their research demonstrated that this innovative scheme offers a more efficient and general numerical tool for the response analyses of entire truss-type periodic structures and even individual structural members. In a parallel development, Luongo and Romeo [173] proposed a modified version of traditional complex wave vector approach for the dynamic analysis, including the free and forced vibrations, of long undamped periodic structures. This version introduced two significant features to address the numerical difficulties encountered by the complex wave vector method. First, the real transfer matrix for state vectors was transformed into a transfer matrix for wave vector, which remained real, thus avoiding an ill-posed problem. Second, the wave vectors were rearranged to let the computation to proceed in the propagation direction of waves, thereby avoiding the transfer matrix ill-conditioning. Numerical examples of an N-span Euler-Bernoulli beam structure validated the efficiency and superiority of this modified wave vector approach. Recently, Ren and Zhou [174] proposed a strain response estimation strategy for the fatigue monitoring of an offshore truss structure, using the state-space formulations and a Kalman filtering process. A small-scale planar truss periodic structure in Figure 4D subjected to deterministic and stochastic excitations was simulated to estimate the effectiveness and integration capacity of the proposed theoretical algorithms with the fatigue monitoring system.
State-Space Based Numerical Methods
In general, the state equations of complex structures can be resolved either analytically or numerically. Traditional state-space analytical methods often encounter challenges when dealing with boundary conditions other than the simply-supported ones, such as the free and clamped end conditions. As a result, over the past two decades, several state-space based numerical methods have been proposed. These methods amalgamate the benefits of both the SSA and the corresponding numerical methods. Examples include the state-space based differential quadrature method (SS-DQM), the state-space based finite element method (SS-FEM), and the state-space based finite difference method (SS-FDM), among others. This section provides a succinct introduction to the state-space based numerical methods and reviews their applications in analyzing the mechanical behaviors of complex structures. These advances are then summarized in Table 4 for easy reference.
TABLE 4
| State-space based numerical methods | Configuration | Reference |
|---|---|---|
| SS-DQM | Beam | [187–195] |
| SS-DQM | Plate | [196–201] |
| SS-DQM | Shell | [202] |
| SS-FEM | Beam | [203–208] |
| SS-FEM | Plate | [209–218] |
| SS-FEM | Shell | [219–221] |
| SS-BEM | Plate | [222] |
| SS-FDM | shell | [223] |
| SS-FSM | Plate | [224] |
| SS-RKP-FSM | Plate | [225] |
| SS-DSC | Beam | [226] |
Summary of state-space based numerical methods to complex structures with different configurations.
Acronyms: SS-DQM, state-space based differential quadrature method; SS-FEM, state-space based finite element method; SS-BEM, state-space based boundary element method; SS-FDM, state-space based finite difference method; SS-FSM, state-space based finite strip method; SS-RKP-FSM, state-space based reproducing kernel particle finite strip method; SS-DSC, state-space based discrete singular convolution.
State-Space Based Differential Quadrature Method
To circumvent the limitation that traditional state-space methods, which struggle with free and clamped boundary conditions, Chen et al. [187–189, 196, 197] proposed a semi-analytical approach that combines state-space formulations with the differential quadrature method (DQM). In this SS-DQM, state-space formulations are established with the transfer direction along the thickness of complex structures, and the state equations are discretized along the in-plane direction. This results in new state equations expressed by state variables at discrete points. The final system algorithm equation can then be obtained by applying various boundary conditions. Since its inception, the SS-DQM has been extensively applied to study the static and dynamic responses of laminated structures in beam, plate, and shell configurations, as summarized in this subsection.
Chen et al. [187] utilized the SS-DQM to present elasticity solutions for the free vibration of thin and thick laminated beams under arbitrary boundary conditions. The agreement between the obtained natural frequencies and those from other works [227, 228] validated the accuracy and effectiveness of the SS-DQM. Numerical results indicated that the SS-DQM predicts frequencies more accurately than the approximate beam theories. Subsequently, they investigated the bending and free vibration of arbitrarily thick beams resting on a Pasternak elastic foundation using the SS-DQM [188]. The SS-DQM was found to be superior to other numerical methods and the beam theories when compared with the exact solutions for simply-supported beams. Moreover, the foundation parameter significantly affects the natural frequencies of the beam system. They further employed this method to examine the free vibration of generally laminated beams, where the principal material axes of orthotropic plies do not coincide with the reference axes [189]. This promoted the applications of the state-space formulations for generally anisotropic materials in structural analysis. Additionally, the SS-DQM was employed by Xu and Wu [190] to investigate the buckling and free vibration of partially interactive composite beams with interlayer slip under various end conditions. This research served as an extension of the work presented in [17], further demonstrating the versatility of the SS-DQM in addressing diverse end conditions.
The SS-DQM has also been used to study the mechanical behaviors of FGM beams. For instance, Lü and Chen [191] studied the free vibration of FGM orthotropic beams with various boundary conditions using the LAT and the orthotropic elasticity theory of plane stress problem. They concluded that the SS-DQM can deal with arbitrary boundary conditions and meanwhile maintain good accuracy even for higher-order mode shapes of thick plates. Furthermore, the method in conjunction with the LAT allows for easy handling of arbitrary material inhomogeneity. Subsequently, they conducted a 2D thermoelasticity analysis of an FGM thick beam as shown in Figure 5A, whose material properties vary continuously and smoothly along the thickness direction, utilizing the SS-DQM along with the LAT [192]. In the numerical calculations, the joint coupling matrices (JCM) were adopted to express the continuity conditions at all mathematical interfaces, thereby avoiding numerical instability. It can be seen from Figure 5B that the excellent agreement between the stress field distributions obtained from the SS-DQM and the exact solutions validated the accuracy of the method. Also, these results could serve as useful benchmarks for analyses of FGM thick beams using other numerical methods. Next, based on the SS-DQM in conjunction with the LAT, they presented semi-analytical elasticity solutions for the bending and thermal deformations of a 2D FGM beam with bi-directional inhomogeneity under various end conditions and subjected to the temperature load [193]. The bi-directional inhomogeneity refers to the Young’s modulus of the beam varying exponentially along both the thickness and longitudinal directions. Simulation results demonstrated that material inhomogeneity along the longitudinal direction significantly affects the deflection of the beam. Moreover, the introduction of bi-directional FGM materials can potentially reduce thermal stresses of the beam when subjected to temperature load. Li and Shi [194] extended the SS-DQM to investigate the free vibration of a functionally graded piezoelectric material (FGPM) beam under different boundary conditions. This was based on the elasticity and piezoelectricity theory in conjunction with the LAT. The strong agreement between the obtained results and those from the FEM validated the accuracy and reliability of the proposed method. Furthermore, the study revealed that the gradient index, boundary conditions, and beam aspect ratio have substantial influences on the fundamental frequency of FGPM beams. Additionally, the SS-DQM based on the elasticity theory was employed by Alibeigloo and Liew [195] to investigate the bending and free vibration of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) beam sandwiched by two piezoelectric layers serving as the sensor and actuator. The effects of the CNT volume fraction, CNT distribution, beam aspect ratio, and boundary conditions on the deflection and natural frequencies were thoroughly examined and discussed.
FIGURE 5
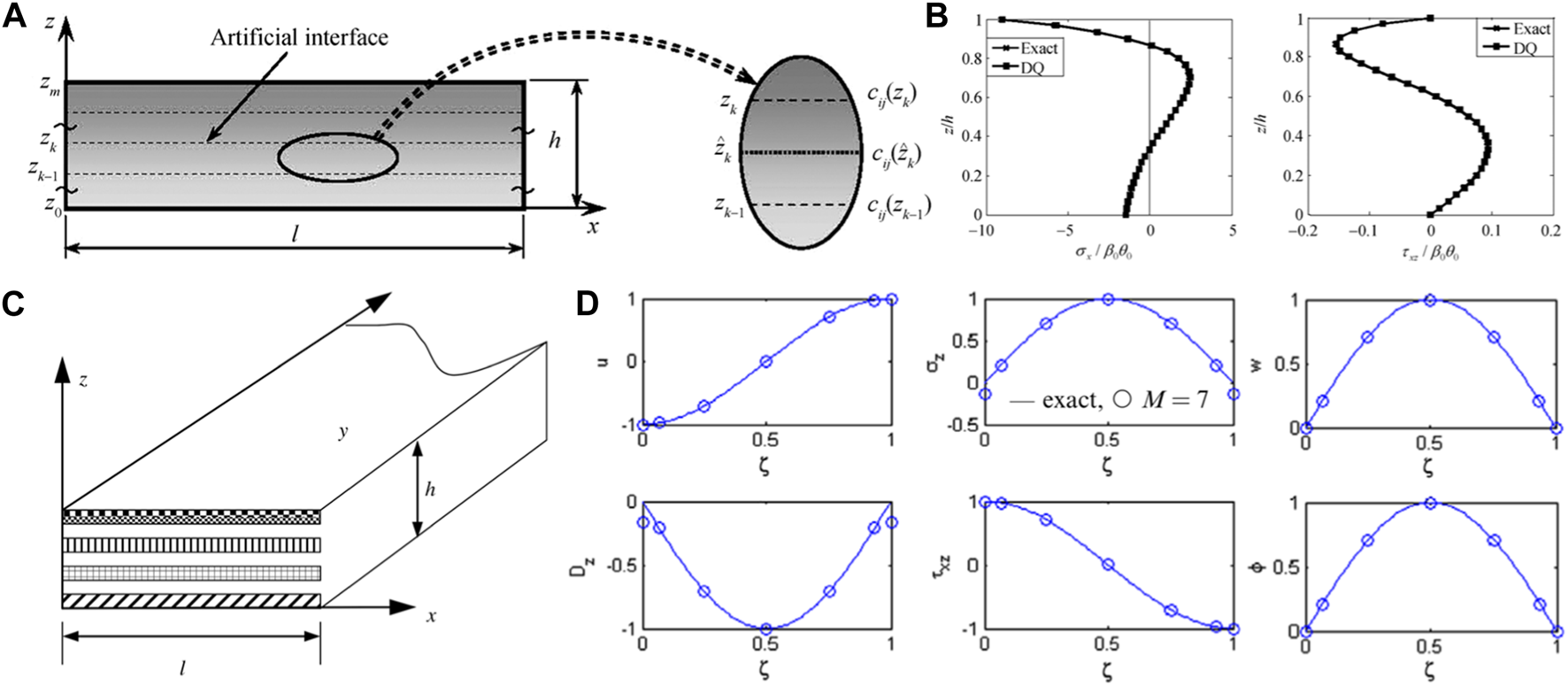
Some cases of applications of the SS-DQM to mechanical analyses of laminated structures: (A) functionally graded material beam and its layerwise approximate model [192]; (B) comparison of stress fields of the beam in (A) along the thickness direction obtained from the SS-DQM and exact solutions; (C) piezoelectric laminated plate in cylindrical bending [199]; (D) comparison of physical fields of the plate in (C) along the thickness direction obtained from the SS-DQM and exact solutions (Reproduced with permission from Lü et al. [192], copyright 2006 by Springer Nature; reproduced with permission from Zhou et al. [199], copyright 2009 by Elsevier).
Apart from the beam configuration, the SS-DQM has also been used to study the mechanical behaviors of complex structures of plate and shell configurations. For example, Chen and Lee [196] performed a free vibration analysis of a cross-ply laminated plate in cylindrical bending under different boundary conditions using the SS-DQM. Numerical results validated the efficiency of the method when dealing with the clamped and free-end conditions. Subsequently, Chen and Lü [197] developed the SS-DQM to investigate the 3D free vibration of a cross-ply laminated plate with one pair of opposite edges simply-supported and with arbitrary boundary conditions at the other pair of opposite edges. Numerous numerical examples of laminated plates, with both symmetric and unsymmetric cross-plies as well as different boundary conditions, were executed to demonstrate the efficiency of the SS-DQM. Lü et al. [198] also investigated the free vibration of generally supported rectangular Kirchhoff plates with internal rigid line supports under generally boundary conditions, utilizing the SS-DQM in conjunction with the JCM. The study underscored the superiority of the developed method over the traditional SSA. Leveraging the SS-DQM developed from the theory of piezoelasticity, Zhou et al. [199] conducted the static and dynamic analyses of orthotropic piezoelectric laminates, as shown in Figure 5C, in cylindrical bending under various boundary conditions. It can be noted from Figure 5D that the physical field distributions along the thickness direction obtained from the SS-DQM with the number of discrete points M = 7 agreed well with those from the exact solutions, validating the accuracy and effectiveness of the semi-analytical method. Subsequently, they extended the SS-DQM to study the effect of interfacial imperfection, described by a general spring layer model, on the mechanical behaviors of this laminate in cylindrical bending [200]. These studies concluded that the SS-DQM is highly accurate and efficient in dealing with non-simple support and imperfect interface problems. Yas and Moloudi [201] employed the SS-DQM to analyze the 3D free vibration of multi-directional FGPM annular plates resting on Pasternak elastic foundation under different boundary conditions. The influences of material gradient index along the thickness and radial directions, the Winkler and shear stiffness of the foundation, and boundary conditions on natural frequencies of the FGPM plate were examined. They found that a decrease in the multi-directional gradient index, an increase in plate thickness, and a change from clamped-clamped to clamped-simple all reduce the natural frequencies of the FGPM plate. The relationships between these factors and frequencies significantly depend on the Winkler and shear elastic coefficients.
Few effort has also been devoted to the mechanical analyses of complex shell structures based on the SS-DQM. Alibeigloo [202] performed static and free vibration analyses of an axisymmetric angle-ply laminated cylindrical shell with various boundary conditions. The accuracy of the method for laminated cylindrical shells was verified by comparing the obtained results with the analytical solutions for simply-supported shells. The effect of different boundary conditions on the static and vibration properties of laminated cylindrical shells was then studied.
State-Space Based Finite Element Method
The 3D finite element method serves as a robust and versatile tool for the mechanical analyses of complex structures under various boundary conditions and subjected to diverse external loads. However, it is widely recognized that the conventional 3D FEM only ensures the continuity of displacement components across all element boundaries. The stresses derived from the displacement components, based on the constitutive equations, are invariably discontinuous across the element boundaries. This discontinuity hampers the accurate prediction of the mechanical behaviors of laminated composite structures, particularly the stress distribution at interlayer interfaces, using the 3D FEM. To address this issue of stress discontinuity inherent in traditional 3D FEM, a semi-analytical method known as state-space based finite element method (SS-FEM) has been recently proposed. This method ingeniously integrates the 3D FEM with the state-space formulations [203–209]. In this approach, a laminated structure is partitioned into finite elements in the in-plane direction, while the displacement and stress distributions along the thickness direction are directly solved from the state equation of the structure. The SS-FEM is characterized by two significant features: 1) it ensures continuous displacement and stress distributions across all interlayer interfaces; and 2) the scale of the final system algorithm equation is independent of the number of layers in the laminated structures. This subsection provides a comprehensive overview of the development of the SS-FEMs for various laminated structures and their applications in the analyses of the mechanical behaviors of these structures.
Ali and Ahankar [203, 204] utilized the SS-FEM to investigate the time-domain dynamic responses of a laminated beam. Their findings were instrumental in developing a novel damage detection method for assessing the composite beam with delamination of varying sizes and positions, based on the Eigen-system Realization Algorithm (ERA). The method demonstrated remarkable accuracy in assessing the size and location of the delamination and predicting the reduction of the bending stiffness of the delamination element, with over 97% accuracy. Similarly, Li and Qing [205] presented a semi-analytical solution for the free vibration of laminated composite beams with delamination, using the SS-FEM based on the modified Hellinger-Reissner (H-R) variational principle. They modeled the delamination between the upper and lower sub-laminates using a non-linear spring-layer model and examined the influences of the delamination size, depth, and boundary conditions on natural frequencies. Their model proved to be a potent and efficient tool for addressing multiple delamination issues in laminated structures. Zhou et al. [206] introduced the SS-FEM for the static response analysis of laminated beams fully sandwiched by piezoelectric actuating layers, based on a modified mixed variational principle. They presented the relationship between the deflection and the secondary converse piezoelectric effect (SCPE), finding that the SCPE significantly affects the deflection of the laminated beam fully covered with piezoelectric actuators. Subsequently, Zhou et al. [207] expanded the aforementioned SS-FEM to investigate the static deformation of laminated curved beams bonded with piezoelectric actuators on the top and bottom surfaces of the substrate. Their model was validated through several complex cases, such as multi-morph piezoelectric curve beams and clamped piezoelectric unimorph C-block beam, and comparison of the obtained results with those from the ANSYS demonstrated the efficiency and accuracy of the new mathematical model. dos Santos et al. [208] proposed a nonlinear SS-FEM based on the von Kármán strain-displacement relation to analyze the nonlinear responses of a laminated beam covered by a piezoelectric sensor, acting as an energy harvester, induced by the flow-structure interaction. The good agreement between the computational results and the experimental data underscored the importance of modeling structural and aerodynamic nonlinearity for accurately depicting the practical electro-aeroelastic behavior of the entire system.
In the context of plate configuration, Zou and Tang [210, 211] presented the semi-analytical solutions for the static deformation and thermal responses of laminated composite plates within the Hamilton system, using the SS-FEM. The quadrilateral element was used as the shape function. Numerical results validated the accuracy and efficiency of the SS-FEM for deformation analyses of laminated plates, particularly for extensive geometry and complex boundary conditions. Built upon the principle of virtual displacement, Sheng and Ye [212] developed the SS-FEM for 3D static deformation analysis of simply-supported three-layered composite plates, using an eight-node quadrilateral element. The comparison of the obtained results with the exact solution in [24] confirmed the accuracy and efficiency of the proposed method. They later applied the SS-FEM to perform stress analysis of orthotropic cross-ply multilayered composite plates, again using an eight-node quadrilateral element [209]. The agreement between the stress fields predicted by the SS-FEM and the existing 3D analytical solutions [229] as well as traditional FEM [230] validated the developed method. Numerical tests also revealed the superiority of the SS-FEM, which provides accurate continuous displacements and transverse stresses along the thickness direction, over the traditional FEM. Ye et al. [213] subsequently conducted the stress analysis of a laminated composite plate with free edges and subjected to transverse and in-plane loads based on the SS-FEM. He et al. [214] explored static displacements and stresses of laminated composite plates under three boundary conditions (free, clamped, and simply-supported) and subjected to thermal load, using the SS-FEM based on the mixed variational principle and an eight-node quadrilateral element. Numerical results again demonstrated the superiority of the SS-FEM over traditional FEMs. Qing et al. [215] developed a general SS-FEM to obtain semi-analytical solutions for the static deformation of magneto-electro-elastic laminated plates, based on the derived modified H-R mixed variational principle for magneto-electro-elastic bodies. They emphasized that the elastic, piezoelectric, and piezomagnetic laminated plates can be considered as special cases of the present model by neglecting certain material constants. They then used this mathematical model, in conjunction with the linear quadrilateral element, to investigate the static response of a simply-supported hybrid laminate and dynamic responses of a clamped aluminum plate with piezoelectric patches [216]. The comparison between the present results and those from the ANSYS validated the efficiency of the developed model. Furthermore, they studied the free vibration of laminated plates reinforced by ribs or beams as the stiffeners [217], and discussed in detail the effect of stiffener height and types on natural frequencies and mode shapes. The same research group also carried out a free vibration analysis of laminated piezoelectric plates with delamination, modeled by a nonlinear spring layer, using the SS-FEM based on the modified H-R variational principle [218]. These numerical simulations indicated that the SS-FEM is a powerful tool for dealing with complex stiffener reinforcement and delamination problems in complex structures.
Additionally, some effort has been invested in applying the SS-FEM to the mechanical analyses of laminated shell structures. For instance, Zhou and Yang [219] conducted a 3D analysis of simply-supported laminated cylindrical shell and panel with arbitrary shell thickness. Their study demonstrated that the proposed method could accurately provide 3D stress and displacement distributions of thin or thick composite shell structures. In a study parallel to the previous research on plate configuration, Sheng and Ye [220] utilized the SS-FEM to generate a semi-analytical solution for stress fields of cross-ply laminated composite shells by using a thin shell element. Simulation results showed that the distributions of stress fields along the thickness direction predicted from the SS-FEM agreed well with those from the exact solutions in [61], suggesting that the method is adept at handling stress problems of laminated shells. Also, the results could serve as a valuable benchmark for testing new shell theory and finite element codes. Built upon the SS-FEM for circular cylindrical shells, Qing et al. [221] proposed a mathematical model for the free vibration of thick double-shell systems, where two cylindrical shells are connected by the springs. Numerical results revealed that the proposed model is not only independent of the thickness and the number of layers in the shell system, but also capable of handling complex support boundaries and the arbitrarily distributed interconnecting springs.
Other State-Space Based Numerical Methods
Apart from the elegant SS-DQM and SS-FEM, other state-space based numerical methods have also been proposed to address structures with unique geometric configurations, such as half-space, or large aspect ratio, or improve the convergence efficiency of numerical methods. In this subsection, we provide a succinct introduction to these state-space based numerical methods. Additionally, we summarize their applications in the mechanical analyses of complex structures.
For instance, Jiang et al. [222] proposed the state-space based boundary element method (SS-BEM) to study the stress distribution of multilayered anisotropic media or half-space under various loads. They employed a procrustean technique to enhance the speed of convergence. On one hand, the SSA can yield the fundamental solutions for orthotropic elastic layers under arbitrary boundary conditions, where the number of equations remains independent of the layer number of the structures. On the other hand, since these fundamental solutions satisfy the boundary conditions and continuity conditions, no elements are required on the boundaries and interfaces. Consequently, when these fundamental solutions are implemented in the spline BEM, the number of elements is significantly reduced without sacrificing numerical accuracy. Undoubtedly, the SS-BEM outperforms the traditional BEM in solving mechanical problems in multilayered anisotropic media, particularly in multilayered half-space. They selected a problem of a spring-supported anisotropic layer containing a uniformly pressurized elliptic cavity under two boundary conditions as the numerical example (schematic of the elastic layer with fixed boundaries was shown in Figure 6A). They found that even though only four elements are used for the entire boundary of the elliptic cavity, the results obtained from the SS-BEM still exhibit good agreement with those from the FEM as shown in Figure 6B. These results validated the accuracy and efficiency of the proposed SS-BEM.
FIGURE 6
Some cases of application of state-space based numerical method to mechanical analyses of laminated structures: (A) an orthotropic elastic layer with an elliptic cavity subjected to uniform internal pressure [222] (B) comparison of the horizontal displacement of the structure in (A) along the horizontal direction predicted by FEM and SS-BEM; (C) cross-section view of 3-ply laminated cylinder [223]; (D) variation of stress fields of the cylinder in (C) versus radius (solid line for analytical solutions and dot for state-space based finite difference method) (Reproduced with permission from Jiang and Lee; copyright 1994 by ASCE; reproduced with permission from Ruddock and Spencer [223], copyright 1997 by The Royal Society).
To address the limitations of the SS-FEM and SS-BEM in analyzing structures with large aspect ratios, which necessitate numerous in-plane elements and consequently result in high computational costs, Ruddock and Spencer [223] introduced the state-space based finite difference method (SS-FDM). This method was specifically developed for the static deformation and stress analyses of laminated or inhomogeneous, anisotropic, elastic, and thermoelastic plates and shells subjected to various mechanical or thermal loads. The SS-FDM employs the finite-difference approximation to discretize the derivatives with respect to the in-plane directions, thereby formulating the elasticity equations as a system of linear first-order ODEs of the stress and displacement variables at the grid-points. By judiciously selecting proper state variables, the state-space formulations were established with the transfer direction along the thickness. Given the inherent efficiency and accuracy of the FDM, the SS-FDM, which is derived from the FDM, also exhibits high efficiency and accuracy, particularly for laminated or inhomogeneous structures. As a demonstration of its effectiveness, Ruddock and Spence conducted a stress analysis of a laminated circular thermoelastic and anisotropic cylinder in plane strain, as shown in Figure 6C, under four external loads. It can be seen from Figure 6D that the results obtained are in excellent agreement with those from the analytical solutions, thereby validating the viability and accuracy of the SS-FDM. However, they also emphasized the need for further research to enhance the robustness of the SS-FDM and to address the challenges associated with the incorporation of boundary conditions.
The finite strip method (FSM) is another well-established numerical method that is particularly suited for the 3D analysis of homogeneous structures with regular geometric configurations [231, 232]. By integrating the FSM and the SSA, Attallah et al. [224] presented a semi-analytical solution of simply-supported laminated composite plates. The FSM was employed to represent the displacement and stress components along the in-plane direction, utilizing polynomial shape functions, while the SSA was used to determine their distributions along the thickness direction of laminated plates. Recently, Khezri introduced a novel variant of FSM, known as the reproducing kernel particle finite strip method (RKP-FSM), to address issues related to abrupt thickness changes or material discontinuities [233]. Subsequently, the same research group [225] proposed an innovative numerical method for the static analysis of thick and orthotropic rectangular laminated composite plates under various boundary conditions. This method was based on the SSA in conjunction with the newly developed RKP-FSM. Similar to the classical FSM, the RKP-FSM was utilized to approximate the in-plane distributions of the displacements and stresses. The SSA was adopted to predict the displacements and stresses in the thickness direction of laminated plates. The SS-FSM and SS-RKP-FSM retained the advantages of the SSA, namely, the number of unknown variables in these methods is independent of the number of plate layers. A series of numerical examples were conducted to evaluate and validate the convergence, accuracy, and robustness of these methods.
Lastly, it is worth noting the state-space based discrete singular convolution (SS-DSC) algorithm proposed by Xin and Hu [226] for the free vibration analysis of laminated magneto-electro-elastic beams. In the SS-DSC approach, the DSC was employed to discretize the length direction of the beam, thereby transforming the original PDEs of a magneto-electro-elastic body into a set of first-order ODEs. By carefully selecting the state variables, the state equation of the beam was established with the transfer direction along the thickness direction. The thickness domain was then analytically solved by using the SSA. The combination of the DSC with the Taylor’s series expansion enabled the implementation of various boundary conditions. Numerical examples demonstrated that the SS-DSC can accurately predict the natural frequencies of laminated composite beams with a low calculation cost. Furthermore, no special arrangement of grid points along the length direction is required, further enhancing the practicality of this method.
Conclusion and Outlooks
Conclusion
This paper presents a comprehensive review of the development and applications of SSAs (also known as transfer matrix methods for state vectors) in the analyses of the mechanical behaviors of complex composite structures of varying configurations, including the beams, plates, shells, and trusses. Utilizing the 3D SSA, simplified SSAs based on structural theories, and state-space based numerical methods, the static deformation and free vibration of laminated structures in beam, plate, and shell forms have been thoroughly investigated. For the sake of completeness, mixed SSAs for the dynamic response analyses of complex periodic structures have also been summarized. It can be generally concluded that SSAs offer a powerful and efficient tool for accurately predicting the static and dynamic responses of laminated and periodic structures. The results obtained could serve as valuable benchmarks for evaluating the developed approximate theoretical methods, numerical methods, and finite element codes. Compared to past research, significant advancements have been made in recent decades, which are summarized as follows:
1) State-space formulations for various material symmetries and geometrical configurations have been established. Leveraging these state-space formulations, transfer matrix methods have been integrated with a range of theoretical or numerical methods, including layerwise approximate technique, wave propagation method, structural theories, finite element method, and differential quadrature method, to facilitate the development of comprehensive SSAs. These approaches provide a more general, efficient, and accurate means of predicting the mechanical behaviors of complex composite and smart structures, particularly in aeronautical applications, under different boundary conditions and subjected to various external loads.
2) Applications of SSAs in the mechanical analyses of complex structures composed of novel smart and composite materials have been documented. These materials include dielectric elastomers, thermo-magneto-electro-elastic coupling materials, and fiber- or graphene-reinforced composite materials. It can be concluded that SSAs can accurately predict the influences of multi-field coupling, material gradient index, external electric, thermal, and mechanical loads, and reinforcement distributions on the mechanical behaviors of these structures.
3) SSAs have also been applied to novel complex structures, such as disordered periodic structures with random unit lengths or random elastic supports, phononic crystal systems with arbitrary geometric configuration, complex structures on various elastic supports or foundations. Novel frequency responses (e.g., high-level response) and wave properties (e.g., stop and pass bands) can be validly revealed and accurately predicted using SSAs.
It is worth mentioning that the state equations of the structures can be solved not only by the transfer matrix method, i.e., the SSA, in this article, but also by the method of reverberation-ray matrix (MRRM) [234–236]. The MRRM is particularly suitable for steady-state or transient response analyses of a truss-type complex structure or a multi-branched frame structure. Different from the system matrix in SSAs, the reverberation-ray matrix consists of two global matrices, namely, the global scattering matrix and the global phase matrix. The detailed differences between the SSA and MRRM can refer to Ref. [237]. In addition, in SSAs, the standard transfer matrix relating the displacements and stresses at the layer top and bottom would become problematic when the layer thickness or frequency increases, resulting in numerical instability of the transfer matrix method. Consequently, the stiffness matrix method (SMM) has been developed to solve this instability [238]. In SMM, the stresses at the top and bottom of the layered structure are expressed by the displacements at the top and bottom through the global stiffness matrix derived through a recursive algorithm based on layer stiffness matrix. In summary, the MRRM and SMM can be a viable alternative to SSAs for the mechanical analyses of certain complex structures in aeronautical and engineering applications.
Outlooks
Despite the substantial advancements that have been made, several significant issues listed in the following remain to be addressed in the future research.
1) SSAs have proven to be efficient and accurate in predicting the mechanical behaviors of low-frequency modes, including bending and extension, in complex composite and smart structures of various geometric configurations. However, high-frequency modes such as thickness-shear and thickness extensional modes exhibit more complex deformation patterns along both in-plane and thickness directions than their low-frequency counterparts [239, 240]. Consequently, the development of SSAs for analyzing the mechanical behaviors of high-frequency modes in these complex structures presents a valuable and intriguing avenue for the future research.
2) State-space techniques have been reported to accurately predict the wave properties of beam-type phononic crystals composed of elastic materials. However, the wave properties of these elastic material phononic crystals remain unalterable once their geometric parameters and configurations are established. Recently, the concept of dielectric elastomer phononic crystals has been introduced, offering the potential for tunable band structures through the application of mechanical and electrical excitations [99, 241, 242]. Consequently, there is a pressing need for the development of appropriate SSAs that can accurately predict the band structures of dielectric elastomer phononic crystals under mechanical and electrical loads. This area of research warrants further investigation.
3) While certain specialized state-space based numerical methods have been proposed to investigate the mechanical behaviors of complex structures of specialized geometric configurations or boundary conditions, their application to such structures remains limited. Consequently, the robustness and versatility of these methods remain uncertain, and potential numerical difficulties may arise in certain applications. This highlights a significant need for the further refinement, rigorous testing, and robustness validation of these state-space based numerical methods. This is a crucial step towards ensuring their reliability and applicability in a wide range of complex structural analyses.
4) The skin-stringer panel system, commonly used in aircraft fuselage, has been modeled as a 1D periodic beam structure on multiple elastic supports. Its dynamic responses have been effectively predicted using the transfer matrix method based on state-space formulations. However, the neglect of the curvature inherent of practical skin panels in the theoretical model may significantly influence the dynamic responses of the actual skin panel system [157]. As a result, investigating the dynamic behaviors of a curved periodic beam structure using the transfer matrix method for state vectors presents a valuable and challenging future research topic.
5) Fluid-solid interaction remains a crucial and challenging issue, particularly due to the extensive use of cylindrical shell and pipeline structures in maritime transportation. There is a pressing need to establish appropriate mechanical models that describe the interaction between the solid structures and various fluids. Built upon these models, the analyses of frequency responses and wave propagation in cylindrical shell structures or periodic pipe structures using SSAs is of vital importance. Such analysis is particularly relevant to the health monitoring and damage warning of these structures, and thus warrants further attention in the future research.
6) With the advancement of micro-electro-mechanical systems (MEMS) and nano-electro-mechanical systems (NEMS), novel laminated structures and devices at the nano or micro scale have been recently fabricated, exhibiting unique, size-dependent behaviors [243, 244]. However, current research on size-dependent behaviors of these miniaturized laminated structures is still in its infancy. Therefore, the development of SSAs in conjunction with various modified continuum theories [243, 245] to explore the size-dependent behaviors of such nanostructures are worth in-depth investigation in future research endeavors.
Statements
Author contributions
ZZ: Conceptualization, writing–original draft, writing–review and editing, funding acquisition. XS: Writing–review and editing. YS: Writing–review and editing. WC: Supervision, conceptualization, writing–review and editing, funding acquisition. All authors contributed to the article and approved the submitted version.
Funding
The work was supported by the National Natural Science Foundation of China (Nos 12192211, 12072315, and 11872329), the Natural Science Foundation of Zhejiang Province (No. LD21A020001), the 111 Project (No. B21034), the National Postdoctoral Program for Innovative Talents (BX2021261), and the China Postdoctoral Science Foundation Funded Project (No. 2022M722745). This work was also partly supported by the specialized research projects of Huanjiang Laboratory, Zhuji, Zhejiang Province.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1.
Li D . Analysis of Composite Laminates: Theories and Their Applications. Amsterdam, Netherlands: Elsevier (2022).
2.
Jawaid M Thariq M , editors. Sustainable Composites for Aerospace Applications. Sawston, United Kingdom: Woodhead publishing (2018).
3.
Rezende MC Botelho EC . O Uso de Compósitos Estruturais na Indústria Aeroespacial. Polímeros (2000) 10:4–10. 10.1590/s0104-14282000000200003
4.
Ezugwu EO . Key Improvements in the Machining of Difficult-To-Cut Aerospace Superalloys. Int J Machine Tools Manufacture (2005) 45(12-13):1353–67. 10.1016/j.ijmachtools.2005.02.003
5.
Loewy RG . Recent Developments in Smart Structures With Aeronautical Applications. Smart Mater Structures (1997) 6(5):R11–42. 10.1088/0964-1726/6/5/001
6.
Chen WQ Wu YF Xu RQ . State Space Formulation for Composite Beam-Columns With Partial Interaction. Composites Sci Tech (2007) 67(11-12):2500–12. 10.1016/j.compscitech.2006.12.013
7.
Zhu W Yang H Liu W Shi B Ling Z Tao H . Experimental Investigation on Innovative Connections for Timber–Concrete Composite Systems. Construction Building Mater (2019) 207:345–56. 10.1016/j.conbuildmat.2019.02.079
8.
Kapania RK Raciti S . Recent Advances in Analysis of Laminated Beams and Plates, Part II: Vibrations and Wave Propagation. AIAA J (1989) 27(7):935–46. 10.2514/3.59909
9.
Noor AK Burton WS . Assessment of Computational Models for Multilayered Composite Shells. Appl Mech Rev (1990) 43:67–97. 10.1115/1.3119162
10.
Thomson WT . Matrix Solution for the Vibration of Nonuniform Beams. J Appl Mech (1950) 17:337–9. 10.1115/1.4010137
11.
Thomson WT . Transmission of Elastic Waves Through a Stratified Solid Medium. J Appl Phys (1950) 21(2):89–93. 10.1063/1.1699629
12.
Kennett B . Seismic Wave Propagation in Stratified Media. The Australian National University: ANU Press (2009).
13.
Bahar LY . A State Space Approach to Elasticity. J Franklin Inst (1975) 299(1):33–41. 10.1016/0016-0032(75)90082-4
14.
Chen WQ Ying J Cai JB Ye GR . Benchmark Solution of Laminated Beams With Bonding Imperfections. AIAA J (2004) 42(2):426–9. 10.2514/1.4776
15.
Ying J Lü CF Chen WQ . Two-Dimensional Elasticity Solutions for Functionally Graded Beams Resting on Elastic Foundations. Compos Structures (2008) 84(3):209–19. 10.1016/j.compstruct.2007.07.004
16.
Bian ZG Lim CW Chen WQ . On Functionally Graded Beams With Integrated Surface Piezoelectric Layers. Compos Structures (2006) 72(3):339–51. 10.1016/j.compstruct.2005.01.005
17.
Xu R Wu YF . Two-Dimensional Analytical Solutions of Simply Supported Composite Beams With Interlayer Slips. Int J Sol Structures (2007) 44(1):165–75. 10.1016/j.ijsolstr.2006.04.027
18.
Xu R Wu YF . Analytical Study of Beams Strengthened by Adhesively Bonded Reinforcement With Variable Properties Using State Space Method. Composites Sci Tech (2009) 69(11-12):1912–8. 10.1016/j.compscitech.2009.04.011
19.
Yan W Ying J Chen WQ . Response of Laminated Adaptive Composite Beams With Viscoelastic Interfaces. Compos Structures (2006) 74(1):70–9. 10.1016/j.compstruct.2005.03.009
20.
Alibeigloo A . Thermoelasticity Analysis of Functionally Graded Beam With Integrated Surface Piezoelectric Layers. Compos Structures (2010) 92(6):1535–43. 10.1016/j.compstruct.2009.10.030
21.
Qian H Qiu Y Lu C Sha X . Analytical Solutions for Laminated Beams Subjected to Non-Uniform Temperature Boundary Conditions. Compos Structures (2022) 282:115044. 10.1016/j.compstruct.2021.115044
22.
Qian H Qiu Y Lu C Yang Y Sha X . Thermal Analysis for Clamped Laminated Beams With Non-Uniform Temperature Boundary Conditions. Thin-Walled Structures (2022) 179:109693. 10.1016/j.tws.2022.109693
23.
Yan W Cai JB Chen WQ . Monitoring Interfacial Defects in a Composite Beam Using Impedance Signatures. J Sound Vibration (2009) 326(1-2):340–52. 10.1016/j.jsv.2009.04.030
24.
Fan JR Ye JQ . An Exact Solution for the Statics and Dynamics of Laminated Thick Plates With Orthotropic Layers. Int J Sol Structures (1990) 26(5-6):655–62.
25.
Chen WQ Cai JB Ye GR . Exact Solutions of Cross-Ply Laminates With Bonding Imperfections. AIAA J (2003) 41(11):2244–50. 10.2514/2.6817
26.
Chen WQ Lee KY . Three-Dimensional Exact Analysis of Angle-Ply Laminates in Cylindrical Bending With Interfacial Damage via State-Space Method. Compos Structures (2004) 64(3-4):275–83. 10.1016/j.compstruct.2003.08.010
27.
Chen WQ Cai JB Ye GR Wang YF . Exact Three-Dimensional Solutions of Laminated Orthotropic Piezoelectric Rectangular Plates Featuring Interlaminar Bonding Imperfections Modeled by a General spring Layer. Int J Sol Structures (2004) 41(18-19):5247–63. 10.1016/j.ijsolstr.2004.03.010
28.
Chen WQ Lee KY . Exact Solution of Angle-Ply Piezoelectric Laminates in Cylindrical Bending With Interfacial Imperfections. Compos Structures (2004) 65(3-4):329–37. 10.1016/j.compstruct.2003.11.008
29.
Chen WQ Ying J Cai JB Ye GR . Benchmark Solution of Imperfect Angle-Ply Laminated Rectangular Plates in Cylindrical Bending With Surface Piezoelectric Layers as Actuator and Sensor. Comput Structures (2004) 82(22):1773–84. 10.1016/j.compstruc.2004.05.011
30.
Fan JR Ye JQ . A Series Solution of the Exact Equation for Thick Orthotropic Plates. Int J Sol Structures (1990) 26(7):773–8.
31.
Zenkour AM . Three-Dimensional Elasticity Solution for Uniformly Loaded Cross-Ply Laminates and Sandwich Plates. J Sandwich Structures Mater (2007) 9(3):213–38. 10.1177/1099636207065675
32.
Chen WQ Lee KY . Time-Dependent Behaviors of Angle-Ply Laminates With Viscous Interfaces in Cylindrical Bending. Eur J Mechanics-A/Solids (2004) 23(2):235–45. 10.1016/j.euromechsol.2003.12.004
33.
Chen WQ Kim GW Lee KY . The Effect of Viscous Interfaces on the Bending of Orthotropic Rectangular Laminates. Compos Structures (2005) 67(3):323–31. 10.1016/j.compstruct.2004.01.014
34.
Qing G Wang F Liu Y . State Space Approach for Energy Release Rate Analysis of Delaminated Laminates With Stiffeners. AIAA J (2011) 49(10):2123–9. 10.2514/1.j050610
35.
Xu K Noor AK Tang YY . Three-Dimensional Solutions for Coupled Thermoelectroelastic Response of Multilayered Plates. Comp Methods Appl Mech Eng (1995) 126(3-4):355–71. 10.1016/0045-7825(95)00825-l
36.
Lee JS Jiang LZ . Exact Electroelastic Analysis of Piezoelectric Laminae via State Space Approach. Int J Sol Structures (1996) 33(7):977–90. 10.1016/0020-7683(95)00083-6
37.
Cheng ZQ Batra RC . Three-Dimensional Asymptotic Analysis of Multiple-Electroded Piezoelectric Laminates. AIAA J (2000) 38(2):317–24. 10.2514/2.959
38.
Benjeddou A Deu JF . Piezoelectric Transverse Shear Actuation and Sensing of Plates, Part 2: Application and Analysis. J Intell Mater Syst Structures (2001) 12(7):451–67. 10.1106/j8dx-r3at-ea6g-85k7
39.
Vel SS Batra RC . Exact Solution for the Cylindrical Bending of Laminated Plates With Embedded Piezoelectric Shear Actuators. Smart Mater Structures (2001) 10(2):240–51. 10.1088/0964-1726/10/2/309
40.
Vel SS Batra RC . Exact Solution for Rectangular Sandwich Plates With Embedded Piezoelectric Shear Actuators. AIAA J (2001) 39(7):1363–73. 10.2514/2.1455
41.
Ding HJ Xu RQ Chi YW Chen WQ . Free Axisymmetric Vibration of Transversely Isotropic Piezoelectric Circular Plates. Int J Sol Structures (1999) 36(30):4629–52.
42.
Wang JG . State Vector Solutions for Nonaxisymmetric Problem of Multilayered Half Space Piezoelectric Medium. Sci China Ser A: Math (1999) 42(12):1323–31. 10.1007/bf02876034
43.
Wang JG Fang S . The State Vector Methods of Axisymmetric Problems for Multilayered Anisotropic Elastic System. Mech Res Commun (1999) 26(6):673–8. 10.1016/s0093-6413(99)00077-4
44.
Wang JG . The State Space Solution of Layered Space Axisymmetric Piezoelectric Media. Acta Mech Sinica (2001) 33(1):115–20.
45.
Wang J Fang S Chen L . The State Vector Methods for Space Axisymmetric Problems in Multilayered Piezoelectric Media. Int J Sol Structures (2002) 39(15):3959–70. 10.1016/s0020-7683(02)00267-6
46.
Sheng HY Wang H Ye JQ . State Space Solution for Thick Laminated Piezoelectric Plates With Clamped and Electric Open-Circuited Boundary Conditions. Int J Mech Sci (2007) 49(7):806–18. 10.1016/j.ijmecsci.2006.11.012
47.
Lezgy-Nazargah M . A Three-Dimensional Exact State-Space Solution for Cylindrical Bending of Continuously Non-Homogenous Piezoelectric Laminated Plates With Arbitrary Gradient Composition. Arch Mech (2015) 67(1):25–51.
48.
Wang J Chen L Fang S . State Vector Approach to Analysis of Multilayered Magneto-Electro-Elastic Plates. Int J Sol Structures (2003) 40(7):1669–80. 10.1016/s0020-7683(03)00027-1
49.
Fan JR Ye JQ . Exact Solutions for Axisymmetric Vibration of Laminated Circular Plates. J Eng Mech (1990) 116(4):920–7.
50.
Qing G Liu Y Guo Q Zhang D . Dynamic Analysis for Three-Dimensional Laminated Plates and Panels With Damping. Int J Mech Sci (2008) 50(1):83–91. 10.1016/j.ijmecsci.2007.05.002
51.
Xu K Noor AK Tang YY . Three-Dimensional Solutions for Free Vibrations of Initially-Stressed Thermoelectroelastic Multilayered Plates. Comp Methods Appl Mech Eng (1997) 141(1-2):125–39. 10.1016/s0045-7825(96)01065-1
52.
Chen WQ Xu RQ Ding HJ . On Free Vibration of a Piezoelectric Composite Rectangular Plate. J Sound Vibration (1998) 4(218):741–8. 10.1006/jsvi.1998.1850
53.
Ding HJ Chen WQ Xu RQ . New State Space Formulations for Transversely Isotropic Piezoelasticity With Application. Mech Res Commun (2000) 27(3):319–26. 10.1016/s0093-6413(00)00098-7
54.
Qing G Xu J Li P Qiu J . A New Efficient Numerical Method and the Dynamic Analysis of Composite Laminates With Piezoelectric Layers. Compos Structures (2007) 78(4):457–67. 10.1016/j.compstruct.2005.11.002
55.
Soldatos KP Ye JQ . Three-Dimensional Static, Dynamic, Thermoelastic and Buckling Analysis of Homogeneous and Laminated Composite Cylinders. Compos Structures (1994) 29(2):131–43. 10.1016/0263-8223(94)90095-7
56.
Ding KW Fan J . Exact Solution for Axisymmetric Problem of Thick Laminated Continuous Closed Cylindrical Shells. Eng Mech (1994) 11(2):8–19. (in Chinese).
57.
Ding KW Tang L Fan J . Exact Analysis for Axisymmetric Vibration and Buckling of the Thick Laminated Closed Cylindrical Shells in a Hamilton System. J Sound Vibration (1997) 206(3):435–41. 10.1006/jsvi.1997.1085
58.
Fan J Zhang J . Analytical Solutions for Thick, Doubly Curved, Laminated Shells. J Eng Mech (1992) 118(7):1338–56. 10.1061/(asce)0733-9399(1992)118:7(1338)
59.
Chen WQ Wang YF Cai JB Ye G . Three-Dimensional Analysis of Cross-Ply Laminated Cylindrical Panels With Weak Interfaces. Int J Sol Structures (2004) 41(9-10):2429–46. 10.1016/j.ijsolstr.2003.12.018
60.
Cai JB Chen WQ Ye GR . Effect of Interlaminar Bonding Imperfections on the Behavior of Angle-Ply Laminated Cylindrical Panels. Composites Sci Tech (2004) 64(12):1753–62. 10.1016/j.compscitech.2003.12.009
61.
Ye JQ Soldatos KP . Three-Dimensional Stress Analysis of Orthotropic and Cross-Ply Laminated Hollow Cylinders and Cylindrical Panels. Comp Methods Appl Mech Eng (1994) 117(3-4):331–51. 10.1016/0045-7825(94)90121-x
62.
Soldatos KP Hadjigeorgiou VP . Three-Dimensional Solution of the Free Vibration Problem of Homogeneous Isotropic Cylindrical Shells and Panels. J Sound Vibration (1990) 137(3):369–84. 10.1016/0022-460x(90)90805-a
63.
Soldatos KP . An Iterative Solution of a Bessel Equation Based on Torsional Vibrations of Orthotropic Hollow Cylinders. J Sound Vibration (1991) 151(1):149–52. 10.1016/0022-460x(91)90657-6
64.
Hawkes TD Soldatos KP . Three-Dimensional Axisymmetric Vibrations of Orthotropic and Cross-Ply Laminated Hollow Cylinders. AIAA J (1992) 30(4):1089–98. 10.2514/3.11031
65.
Ye JQ Soldatos KP . Three-Dimensional Vibration of Laminated Cylinders and Cylindrical Panels With Symmetric or Antisymmetric Cross-Ply Lay-Up. Composites Eng (1994) 4(4):429–44. 10.1016/s0961-9526(09)80016-6
66.
Ding K Tang L . Three-Dimensional Free Vibration of Thick Laminated Cylindrical Shells With Clamped Edges. J Sound Vibration (1999) 1(220):171–7. 10.1006/jsvi.1998.1897
67.
Chen WQ Bian ZG Ding HJ . Three-Dimensional Vibration Analysis of Fluid-Filled Orthotropic FGM Cylindrical Shells. Int J Mech Sci (2004) 46(1):159–71. 10.1016/j.ijmecsci.2003.12.005
68.
Zhu F Wu B Destrade M Chen W . Electrostatically Tunable Axisymmetric Vibrations of Soft Electro-Active Tubes. J Sound Vibration (2020) 483:115467. 10.1016/j.jsv.2020.115467
69.
Ye JQ Soldatos KP . Three-Dimensional Buckling Analysis of Laminated Composite Hollow Cylinders and Cylindrical Panels. Int J Sol Structures (1995) 32(13):1949–62. 10.1016/0020-7683(94)00217-k
70.
Talebitooti R Ahmadi R Shojaeefard MH . Three-Dimensional Wave Propagation on Orthotropic Cylindrical Shells With Arbitrary Thickness Considering State Space Method. Compos Structures (2015) 132:239–54. 10.1016/j.compstruct.2015.05.023
71.
Wu B Su Y Chen W Zhang C . On Guided Circumferential Waves in Soft Electroactive Tubes Under Radially Inhomogeneous Biasing fields. J Mech Phys Sol (2017) 99:116–45. 10.1016/j.jmps.2016.11.004
72.
Wu B Su Y Liu D Chen W Zhang C . On Propagation of Axisymmetric Waves in Pressurized Functionally Graded Elastomeric Hollow Cylinders. J Sound Vibration (2018) 421:17–47. 10.1016/j.jsv.2018.01.055
73.
Chen WQ Ding HJ . A State-Space-Based Stress Analysis of a Multilayered Spherical Shell With Spherical Isotropy. J Appl Mech (2001) 68(1):109–14. 10.1115/1.1343913
74.
Chen WQ Ding HJ Xu R . Three-Dimensional Static Analysis of Multi-Layered Piezoelectric Hollow Spheres via the State Space Method. Int J Sol Structures (2001) 38(28-29):4921–36. 10.1016/s0020-7683(00)00314-0
75.
Chen WQ Ding HJ . Free Vibration of Multi-Layered Spherically Isotropic Hollow Spheres. Int J Mech Sci (2001) 43(3):667–80. 10.1016/s0020-7403(00)00044-8
76.
Chen WQ Wang LZ Lu Y . Free Vibrations of Functionally Graded Piezoceramic Hollow Spheres With Radial Polarization. J Sound Vibration (2002) 251(1):103–14. 10.1006/jsvi.2001.3973
77.
Mao R Wu B Carrera E Chen W . Electrostatically Tunable Small-Amplitude Free Vibrations of Pressurized Electro-Active Spherical Balloons. Int J Non-Linear Mech (2019) 117:103237. 10.1016/j.ijnonlinmec.2019.103237
78.
Cheng ZQ Lim CW Kitipornchai S . Three-Dimensional Asymptotic Approach to Inhomogeneous and Laminated Piezoelectric Plates. Int J Sol Structures (2000) 37(23):3153–75. 10.1016/s0020-7683(99)00036-0
79.
He XQ Ng TY Sivashanker S Liew KM . Active Control of FGM Plates With Integrated Piezoelectric Sensors and Actuators. Int J Sol Structures (2001) 38(9):1641–55. 10.1016/s0020-7683(00)00050-0
80.
Liew KM He XQ Ng TY Kitipornchai S . Active Control of FGM Shells Subjected to a Temperature Gradient via Piezoelectric Sensor/Actuator Patches. Int J Numer Methods Eng (2002) 55(6):653–68. 10.1002/nme.519
81.
Pagano NJ . Exact Solutions for Composite Laminates in Cylindrical Bending. J Compos Mater (1969) 3(3):398–411. 10.1177/002199836900300304
82.
Pagano NJ . Exact Solutions for Rectangular Bidirectional Composites and Sandwich Plates. J Compos Mater (1970) 4(1):20–34. 10.1177/002199837000400102
83.
Pagano NJ . Influence of Shear Coupling in Cylindrical. Bending of Anisotropic Laminates. J Compos Mater (1970) 4(3):330–43. 10.1177/002199837000400305
84.
Pagano NJ Hatfield SJ . Elastic Behavior of Multilayered Bidirectional Composites. AIAA J (1972) 10(7):931–3.
85.
Heyliger P . Static Behavior of Laminated Elastic/Piezoelectric Plates. AIAA J (1994) 32(12):2481–4. 10.2514/3.12321
86.
Heyliger P Brooks S . Free Vibration of Piezoelectric Laminates in Cylindrical Bending. Int J Sol Structures (1995) 32(20):2945–60. 10.1016/0020-7683(94)00270-7
87.
Heyliger P Brooks S . Exact Solutions for Laminated Piezoelectric Plates in Cylindrical Bending. J Appl Mech (1996) 63(4):903–10. 10.1115/1.2787245
88.
Heyliger P . Exact Solutions for Simply Supported Laminated Piezoelectric Plates. J Appl Mech (1997) 64(2):299–306. 10.1115/1.2787307
89.
Cheng ZQ Kennedy D Williams WF . Effect of Interfacial Imperfection on Buckling and Bending Behavior of Composite Laminates. AIAA J (1996) 34(12):2590–5. 10.2514/3.13443
90.
Benjeddou A Deu JF . Piezoelectric Transverse Shear Actuation and Sensing of Plates, Part 1: A Three-Dimensional Mixed State Space Formulation. J Intell Mater Syst Structures (2001) 12(7):435–49. 10.1177/10453890122145258
91.
Pan E . Exact Solution for Simply Supported and Multilayered Magneto-Electro-Elastic Plates. J Appl Mech (2001) 68(4):608–18. 10.1115/1.1380385
92.
Chen WQ Ding HJ . Natural Frequencies of Fluid-Filled Transversely Isotropic Cylindrical Shells. Int J Mech Sci (1999) 41(6):677–84. 10.1016/s0020-7403(98)00088-5
93.
Raju PP . On Shallow Shells of Transversely Isotropic Materials. J Press Vessel Tech (1975) 97(3):185–91. 10.1115/1.3454293
94.
Maiti M . Stresses in Anisotropic Nonhomogeneous Sphere. J Eng Mech Division (1975) 101(1):101–8. 10.1061/jmcea3.0001985
95.
Montagner JP Anderson DL . Constrained Reference Mantle Model. Phys earth Planet Interiors (1989) 58(2-3):205–27. 10.1016/0031-9201(89)90055-1
96.
Ding ZY Zou DQ Ding HJ . A Study of Effects of the Earth's Radial Anisotropy on the Tidal Stress Field. Tectonophysics (1996) 258(1-4):103–14. 10.1016/0040-1951(95)00186-7
97.
Heyliger P Wu YC . Electroelastic Fields in Layered Piezoelectric Spheres. Int J Eng Sci (1999) 37(2):143–61. 10.1016/s0020-7225(98)00068-8
98.
Pelrine R Kornbluh R Pei Q Joseph J . High-Speed Electrically Actuated Elastomers With Strain Greater Than 100%. Science (2000) 287(5454):836–9. 10.1126/science.287.5454.836
99.
Zhao Z Chen Y Hu X Bao R Wu B Chen WQ . Vibrations and Waves in Soft Dielectric Elastomer Structures. Int J Mech Sci (2022) 239:107885. 10.1016/j.ijmecsci.2022.107885
100.
Khdeir AA Reddy JN . Free Vibration of Cross-Ply Laminated Beams With Arbitrary Boundary Conditions. Int J Eng Sci (1994) 32(12):1971–80. 10.1016/0020-7225(94)90093-0
101.
Khdeir AA Redd JN . Buckling of Cross-Ply Laminated Beams With Arbitrary Boundary Conditions. Compos Structures (1997) 37(1):1–3. 10.1016/s0263-8223(97)00048-2
102.
Trinh LC Vo TP Thai HT Nguyen TK . An Analytical Method for the Vibration and Buckling of Functionally Graded Beams Under Mechanical and Thermal Loads. Composites B: Eng (2016) 100:152–63. 10.1016/j.compositesb.2016.06.067
103.
Khdeir AA . Dynamic Response of Antisymmetric Cross-Ply Laminated Composite Beams With Arbitrary Boundary Conditions. Int J Eng Sci (1996) 34(1):9–19. 10.1016/0020-7225(95)00080-1
104.
Trinh LC Vo TP Osofero AI Lee J . Fundamental Frequency Analysis of Functionally Graded Sandwich Beams Based on the State Space Approach. Compos Structures (2016) 156:263–75. 10.1016/j.compstruct.2015.11.010
105.
Khdeir AA Reddy JN . An Exact Solution for the Bending of Thin and Thick Cross-Ply Laminated Beams. Compos Structures (1997) 37(2):195–203. 10.1016/s0263-8223(97)80012-8
106.
Khdeir AA Reddy JN . Jordan Canonical Form Solution for Thermally Induced Deformations of Cross-Ply Laminated Composite Beams. J Therm Stresses (1999) 22(3):331–46.
107.
Khdeir AA . Thermal Buckling of Cross-Ply Laminated Composite Beams. Acta Mechanica (2001) 149(1-4):201–13. 10.1007/bf01261672
108.
Aldraihem OJ Khdeir AA . Smart Beams With Extension and Thickness-Shear Piezoelectric Actuators. Smart Mater Structures (2000) 9(1):1–9. 10.1088/0964-1726/9/1/301
109.
Sahmani S Ansari R . Nonlocal Beam Models for Buckling of Nanobeams Using State-Space Method Regarding Different Boundary Conditions. J Mech Sci Tech (2011) 25:2365–75. 10.1007/s12206-011-0711-6
110.
Pota HR Alberts TE . Multivariable Transfer Functions for a Slewing Piezoelectric Laminate Beam. J Dynamic Syst Meas Control (1995) 117(3):352–9. 10.1115/1.2799126
111.
Palmeri A Adhikari S . A Galerkin-Type State-Space Approach for Transverse Vibrations of Slender Double-Beam Systems With Viscoelastic Inner Layer. J Sound Vibration (2011) 330(26):6372–86. 10.1016/j.jsv.2011.07.037
112.
Palmeri A Ntotsios E . Transverse Vibrations of Viscoelastic Sandwich Beams via Galerkin-Based State-Space Approach. J Eng Mech (2016) 142(7):04016036. 10.1061/(asce)em.1943-7889.0001069
113.
Li Y Xiong F Xie L Sun L . State-Space Approach for Transverse Vibration of Double-Beam Systems. Int J Mech Sci (2021) 189:105974. 10.1016/j.ijmecsci.2020.105974
114.
Khdeir AA Aldraihem OJ . Free Vibration of Sandwich Beams With Soft Core. Compos Structures (2016) 154:179–89. 10.1016/j.compstruct.2016.07.045
115.
Srinivasan R Dattaguru B Singh G . Exact Solutions for Laminated Composite Beams Using a Unified State Space Formulation. Int J Comput Methods Eng Sci Mech (2019) 20(4):319–34. 10.1080/15502287.2019.1644394
116.
Ramaprasad S Dattaguru B Singh G . Exact Solutions for Thin-Walled Composite Open Section Beams Using a Unified State Space Coupled Field Formulation. Mech Based Des Structures Machines (2022) 51(11):5983–6007. 10.1080/15397734.2021.2024846
117.
Fazeli S Stokes-Griffin C Gilbert J Compston P . An Analytical Solution for the Vibrational Response of Stepped Smart Cross-Ply Laminated Composite Beams With Experimental Validation. Compos Structures (2021) 266:113823. 10.1016/j.compstruct.2021.113823
118.
Khdeir AA . A Remark on the State-Space Concept Applied to Bending, Buckling and Free Vibration of Composite Laminates. Comput Structures (1996) 59(5):813–7. 10.1016/0045-7949(95)00330-4
119.
Khdeir AA Reddy JN . Analytical Solutions of Refined Plate Theories of Cross-Ply Composite Laminates. J Press Vessel Tech (1991) 113(4):570–8. 10.1115/1.2928797
120.
Khdeir AA . Comparison Between Shear Deformable and Kirchhoff Theories for Bending, Buckling and Vibration of Antisymmetric Angle-Ply Laminated Plates. Compos Structures (1989) 13(3):159–72. 10.1016/0263-8223(89)90001-9
121.
Khdeir AA . An Exact Approach to the Elastic State of Stress of Shear Deformable Antisymmetric Angle-Ply Laminated Plates. Compos Structures (1989) 11(4):245–58. 10.1016/0263-8223(89)90090-1
122.
Librescu L Khdeir AA . Analysis of Symm≐tric Cross-Ply Laminated Elastic Plates Using a Higher-Order Theory: Part I—Stress and Displacement. Compos Structures (1988) 9(3):189–213. 10.1016/0263-8223(88)90014-1
123.
Xing Y Xiang W . Analytical Solution Methods for Eigenbuckling of Symmetric Cross-Ply Composite Laminates. Chin J Aeronautics (2017) 30(1):282–91. 10.1016/j.cja.2016.12.027
124.
Khdeir AA . Free Vibration of Antisymmetric Angle-Ply Laminated Plates Including Various Boundary Conditions. J Sound Vibration (1988) 122(2):377–88. 10.1016/s0022-460x(88)80361-4
125.
Khdeir AA . Stability of Antisymmetric Angle-Ply Laminated Plates. J Eng Mech (1989) 115(5):952–62. 10.1061/(asce)0733-9399(1989)115:5(952)
126.
Khdeir AA Librescu L . Analysis of Symmetric Cross-Ply Laminated Elastic Plates Using a Higher-Order Theory: Part II—Buckling and Free Vibration. Compos Structures (1988) 9(4):259–77. 10.1016/0263-8223(88)90048-7
127.
Khdeir AA . Free Vibration and Buckling of Symmetric Cross-Ply Laminated Plates by an Exact Method. J Sound Vibration (1988) 126(3):447–61. 10.1016/0022-460x(88)90223-4
128.
Khdeir AA . Free Vibration and Buckling of Unsymmetric Cross-Ply Laminated Plates Using a Refined Theory. J Sound Vibration (1989) 128(3):377–95. 10.1016/0022-460x(89)90781-5
129.
Trinh LC Vo TP Thai HT Nguyen TK Keerthan P . State-Space Levy Solution for Size-Dependent Static, Free Vibration and Buckling Behaviours of Functionally Graded Sandwich Plates. Composites Part B: Eng (2018) 149:144–64. 10.1016/j.compositesb.2018.05.017
130.
Zhang LW Song ZG Liew KM . State-Space Levy Method for Vibration Analysis of FG-CNT Composite Plates Subjected to In-Plane Loads Based on Higher-Order Shear Deformation Theory. Compos Structures (2015) 134:989–1003. 10.1016/j.compstruct.2015.08.138
131.
Lv QH Lei ZX Zhang Y . Vibration Characteristic of Moderately Thick Graphene Reinforced Composite Functionally Graded Plate Based on State-Space Levy Method Combined With Higher Order Shear Deformation Theory. IOP Conf Ser Mater Sci Eng (2019) 531(1):012002. 10.1088/1757-899x/531/1/012002
132.
Sobhy M . Hygrothermal Deformation of Orthotropic Nanoplates Based on the State-Space Concept. Composites Part B: Eng (2015) 79:224–35. 10.1016/j.compositesb.2015.04.042
133.
Demirhan PA Taskin V . Bending and Free Vibration Analysis of Levy-Type Porous Functionally Graded Plate Using State Space Approach. Composites Part B: Eng (2019) 160:661–76. 10.1016/j.compositesb.2018.12.020
134.
Rouzegar J Salmanpour N Abad F Li L . An Analytical State-Space Solution for Free Vibration of Sandwich Piezoelectric Plate With Functionally Graded Core. Scientia Iranica (2022) 29(2):502–33.
135.
Khdeir AA Reddy JN Frederick D . A Study of Bending, Vibration and Buckling of Cross-Ply Circular Cylindrical Shells With Various Shell Theories. Int J Eng Sci (1989) 27(11):1337–51. 10.1016/0020-7225(89)90058-x
136.
Khdeir AA Reddy JN . Influence of Edge Conditions on the Modal Characteristics of Cross-Ply Laminated Shells. Comput Structures (1990) 34(6):817–26. 10.1016/0045-7949(90)90352-3
137.
Dozio L . A Hierarchical Formulation of the State-Space Levy's Method for Vibration Analysis of Thin and Thick Multilayered Shells. Composites Part B: Eng (2016) 98:97–107. 10.1016/j.compositesb.2016.05.022
138.
Hosseini-Hashemi S Abaei AR Ilkhani MR . Free Vibrations of Functionally Graded Viscoelastic Cylindrical Panel Under Various Boundary Conditions. Compos Structures (2015) 126:1–15. 10.1016/j.compstruct.2015.02.031
139.
Razgordanisharahi A Ghassabi AA Hellmich C . Free Vibration Analysis of Cylindrical Honeycomb Sandwich Panels Using State-Space Levy Method. Thin-Walled Structures (2023) 182:110308. 10.1016/j.tws.2022.110308
140.
Civalek Ö Kiracioglu O . Free Vibration Analysis of Timoshenko Beams by DSC Method. Int J Numer Methods Biomed Eng (2010) 26(12):1890–8. 10.1002/cnm.1279
141.
Alberts TE Colvin JA . Observations on the Nature of Transfer Functions for Control of Piezoelectric Laminates. J Intell Mater Syst Structures (1991) 2(4):528–41. 10.1177/1045389x9100200407
142.
Ansari R Sahmani S Rouhi H . Rayleigh–Ritz Axial Buckling Analysis of Single-Walled Carbon Nanotubes With Different Boundary Conditions. Phys Lett A (2011) 375(9):1255–63. 10.1016/j.physleta.2011.01.046
143.
Wang M Xu YG Qiao P Li ZM . A Two-Dimensional Elasticity Model for Bending and Free Vibration Analysis of Laminated Graphene-Reinforced Composite Beams. Compos Structures (2019) 211:364–75. 10.1016/j.compstruct.2018.12.033
144.
Chandrashekara S Santhoshi U . Natural Frequencies of Cross-Ply Laminates by State Space Approach. J Sound Vibration (1990) 136(3):413–24. 10.1016/0022-460x(90)90453-7
145.
Reddy JN . Energy and Variational Methods in Applied Mechanics. United States: John Wiley (1984).
146.
Reddy JN . A Simple Higher-Order Theory for Laminated Composite Plates. J Appl Mech (1984) 51(4):745–52. 10.1115/1.3167719
147.
Khdeir AA . Analytical Solutions for the Statics and Dynamics of Rectangular Laminated Composite Plates Using Shearing Deformation Theories. United States: Virginia Polytechnic Institute and State University (1986).
148.
Xiang Y Liew KM Kitipornchai S . Exact Buckling Solutions for Composite Laminates: Proper Free Edge Conditions Under In-Plane Loadings. Acta Mechanica (1996) 117(1-4):115–28. 10.1007/bf01181041
149.
Rezaei AS Saidi AR Abrishamdari M Pour Mohammadi MH . Natural Frequencies of Functionally Graded Plates With Porosities via a Simple Four Variable Plate Theory: An Analytical Approach. Thin-Walled Structures (2017) 120:366–77. 10.1016/j.tws.2017.08.003
150.
Jin G Su Z Shi S Ye T Gao S . Three-Dimensional Exact Solution for the Free Vibration of Arbitrarily Thick Functionally Graded Rectangular Plates With General Boundary Conditions. Compos Structures (2014) 108:565–77. 10.1016/j.compstruct.2013.09.051
151.
Zaoui FZ Ouinas D Tounsi A . New 2D and Quasi-3D Shear Deformation Theories for Free Vibration of Functionally Graded Plates on Elastic Foundations. Composites Part B: Eng (2019) 159:231–47. 10.1016/j.compositesb.2018.09.051
152.
Fazzolari FA . A Refined Dynamic Stiffness Element for Free Vibration Analysis of Cross-Ply Laminated Composite Cylindrical and Spherical Shallow Shells. Composites Part B: Eng (2014) 62:143–58. 10.1016/j.compositesb.2014.02.021
153.
Hosseini-Hashemi S Fadaee M . On the Free Vibration of Moderately Thick Spherical Shell Panel—A New Exact Closed-Form Procedure. J Sound Vibration (2011) 330(17):4352–67. 10.1016/j.jsv.2011.04.011
154.
Noor AK Anderson MS Greene WH . Continuum Models for Beam-And Platelike Lattice Structures. AIAA J (1978) 16(12):1219–28. 10.2514/3.61036
155.
Ayre RS Jacobsen LS . Natural Frequencies of Continuous Beams of Uniform Span Length. J Appl Mech (1950) 17:391–5. 10.1115/1.4010165
156.
Miles JW . Vibrations of Beams on Many Supports. J Eng Mech Division (1956) 82(1):1–9. 10.1061/jmcea3.0000001
157.
Lin YK McDaniel TJ . Dynamics of Beam-Type Periodic Structures. J Eng Industry (1969) 91:1133–41. 10.1115/1.3591761
158.
Vaicaitis R Doi K Lin YK . Spatial Decay in the Response of Damped Periodic Beam. J Aircraft (1972) 9(1):91–3. 10.2514/3.44324
159.
Lin YK Yang JN . Free Vibration of a Disordered Periodic Beam. J Appl Mech (1974) 41(2):383–91. 10.1115/1.3423298
160.
Yang JN Lin YK . Frequency Response Functions of a Disordered Periodic Beam. J Sound Vibration (1975) 38(3):317–40. 10.1016/s0022-460x(75)80050-2
161.
Vaicaitis R Lin YK . Response of Finite Periodic Beam to Turbulent Boundary-Layer Pressure Excitation. AIAA J (1972) 10(8):1020–4. 10.2514/3.50288
162.
Yeh JY Chen LW . Wave Propagations of a Periodic Sandwich Beam by FEM and the Transfer Matrix Method. Compos Structures (2006) 73(1):53–60. 10.1016/j.compstruct.2005.01.026
163.
Assis GF Beli D de Miranda EJ Jr Camino JF Dos Santos JMC Arruda JRF . Computing the Complex Wave and Dynamic Behavior of One-Dimensional Phononic Systems Using a State-Space Formulation. Int J Mech Sci (2019) 163:105088. 10.1016/j.ijmecsci.2019.105088
164.
Lin YK Zhang R Yong Y . Multiply Supported Pipeline Under Seismic Wave Excitations. J Eng Mech (1990) 116(5):1094–108. 10.1061/(asce)0733-9399(1990)116:5(1094)
165.
Cai GQ Lin YK . Localization of Wave Propagation in Disordered Periodic Structures. AIAA J (1991) 29(3):450–6. 10.2514/3.10599
166.
Qiu CX Lin YK . Localization of Mono-And Multichannel Waves in Disordered Periodic Systems. J Eng Mech (1997) 123(8):830–6. 10.1061/(asce)0733-9399(1997)123:8(830)
167.
Cai GQ Lin YK . Statistical Distribution of Frequency Response in Disordered Periodic Structures. AIAA J (1992) 30(5):1400–7. 10.2514/3.11076
168.
Saeed HM Vestroni F . Simulation of Combined Systems by Periodic Structures: The Wave Transfer Matrix Approach. J Sound Vibration (1998) 213(1):55–74. 10.1006/jsvi.1997.1497
169.
Romeo F Paolone A . Wave Propagation in Three-Coupled Periodic Structures. J Sound Vibration (2007) 301(3-5):635–48. 10.1016/j.jsv.2006.10.017
170.
Yong Y Lin YK . Propagation of Decaying Waves in Periodic and Piecewise Periodic Structures of Finite Length. J Sound Vibration (1989) 129(1):99–118. 10.1016/0022-460x(89)90538-5
171.
Yong Y Lin YK . Dynamics of Complex Truss-Type Space Structures. AIAA J (1990) 28(7):1250–8. 10.2514/3.25202
172.
Yong Y Lin YK . Dynamic Response Analysis of Truss-Type Structural Networks: A Wave Propagation Approach. J Sound Vibration (1992) 156(1):27–45. 10.1016/0022-460x(92)90810-k
173.
Luongo A Romeo F . Real Wave Vectors for Dynamic Analysis of Periodic Structures. J Sound Vibration (2005) 279(1-2):309–25. 10.1016/j.jsv.2003.11.011
174.
Ren P Zhou Z . Strain Response Estimation for the Fatigue Monitoring of an Offshore Truss Structure. Pac Sci Rev (2014) 16(1):29–35. 10.1016/j.pscr.2014.08.005
175.
Cai GQ Lin YK . Wave Propagation and Scattering in Structural Networks. J Eng Mech (1991) 117(7):1555–74. 10.1061/(asce)0733-9399(1991)117:7(1555)
176.
Lin YK Donaldson BK . A Brief Survey of Transfer Matrix Techniques With Special Reference to the Analysis of Aircraft Panels. J Sound Vibration (1969) 10(1):103–43. 10.1016/0022-460x(69)90132-1
177.
Heckl MA . Investigations on the Vibrations of Grillages and Other Simple Beam Structures. The J Acoust Soc America (1964) 36(7):1335–43. 10.1121/1.1919206
178.
Mead DJ . Free Wave Propagation in Periodically Supported, Infinite Beams. J Sound Vibration (1970) 11(2):181–97. 10.1016/s0022-460x(70)80062-1
179.
Gupta GS . Natural Flexural Waves and the Normal Modes of Periodically-Supported Beams and Plates. J Sound Vibration (1970) 13(1):89–101. 10.1016/s0022-460x(70)80082-7
180.
Mead D . A General Theory of Harmonic Wave Propagation in Linear Periodic Systems With Multiple Coupling. J Sound Vibration (1973) 27(2):235–60. 10.1016/0022-460x(73)90064-3
181.
Mead DJ . Wave Propagation and Natural Modes in Periodic Systems: I. Mono-Coupled Systems. J Sound Vibration (1975) 40(1):1–18. 10.1016/s0022-460x(75)80227-6
182.
Mead D . Wave Propagation and Natural Modes in Periodic Systems: II. Multi-Coupled Systems, With and Without Damping. J Sound Vibration (1975) 40(1):19–39. 10.1016/s0022-460x(75)80228-8
183.
Mead DJ Markuš Š . Coupled Flexural-Longitudinal Wave Motion in a Periodic Beam. J Sound Vibration (1983) 90(1):1–24. 10.1016/0022-460x(83)90399-1
184.
Zhu L Elishakoff I Lin YK . Free and Forced Vibrations of Periodic Multispan Beams. Shock and Vibration (1994) 1(3):217–32. 10.1155/1994/961272
185.
Lin YK . Dynamics of Disordered Periodic Structures. Appl Mech Rev (1996) 49(2):57–64. 10.1115/1.3101888
186.
Von Flotow AH . Disturbance Propagation in Structural Networks. J Sound Vibration (1986) 106(3):433–50. 10.1016/0022-460x(86)90190-2
187.
Chen WQ Lü CF Bian EZ . Elasticity Solution for Free Vibration of Laminated Beams. Compos Structures (2003) 62(1):75–82. 10.1016/s0263-8223(03)00086-2
188.
Chen WQ Lü CF Bian ZG . A Mixed Method for Bending and Free Vibration of Beams Resting on a Pasternak Elastic Foundation. Appl Math Model (2004) 28(10):877–90. 10.1016/j.apm.2004.04.001
189.
Chen WQ Lü CF Bian ZG . Free Vibration Analysis of Generally Laminated Beams via State-Space-Based Differential Quadrature. Compos Structures (2004) 63(3-4):417–25.
190.
Xu R Wu YF . Free Vibration and Buckling of Composite Beams With Interlayer Slip by Two-Dimensional Theory. J Sound Vibration (2008) 313(3-5):875–90. 10.1016/j.jsv.2007.12.029
191.
Lü CF Chen WQ . Free Vibration of Orthotropic Functionally Graded Beams With Various End Conditions. Struct Eng Mech (2005) 20(4):465–76. 10.12989/sem.2005.20.4.465
192.
Lü CF Chen W Zhong Z . Two-Dimensional Thermoelasticity Solution for Functionally Graded Thick Beams. Sci China Ser G: Phys Mech Astron (2006) 49:451–60. 10.1007/s11433-006-0451-2
193.
Lü CF Chen WQ Xu RQ Lim CW . Semi-Analytical Elasticity Solutions for Bi-Directional Functionally Graded Beams. Int J Sol Structures (2008) 45(1):258–75. 10.1016/j.ijsolstr.2007.07.018
194.
Li Y Shi Z . Free Vibration of a Functionally Graded Piezoelectric Beam via State-Space Based Differential Quadrature. Compos Structures (2009) 87(3):257–64. 10.1016/j.compstruct.2008.01.012
195.
Alibeigloo A Liew KM . Elasticity Solution of Free Vibration and Bending Behavior of Functionally Graded Carbon Nanotube-Reinforced Composite Beam With Thin Piezoelectric Layers Using Differential Quadrature Method. Int J Appl Mech (2015) 7(01):1550002. 10.1142/s1758825115400025
196.
Chen WQ Lee KY . On Free Vibration of Cross-Ply Laminates in Cylindrical Bending. J Sound Vibration (2004) 273(3):667–76. 10.1016/j.jsv.2003.08.003
197.
Chen WQ Lü CF . 3D Free Vibration Analysis of Cross-Ply Laminated Plates With One Pair of Opposite Edges Simply Supported. Compos Structures (2005) 69(1):77–87. 10.1016/j.compstruct.2004.05.015
198.
Lü CF Zhang ZC Chen WQ . Free Vibration of Generally Supported Rectangular Kirchhoff Plates: State-Space-Based Differential Quadrature Method. Int J Numer Methods Eng (2007) 70(12):1430–50. 10.1002/nme.1929
199.
Zhou YY Chen WQ Lü CF Wang J . Free Vibration of Cross-Ply Piezoelectric Laminates in Cylindrical Bending With Arbitrary Edges. Compos Structures (2009) 87(1):93–100. 10.1016/j.compstruct.2008.01.002
200.
Zhou YY Chen WQ Lü CF . Semi-Analytical Solution for Orthotropic Piezoelectric Laminates in Cylindrical Bending With Interfacial Imperfections. Compos Structures (2010) 92(4):1009–18. 10.1016/j.compstruct.2009.09.048
201.
Yas MH Moloudi N . Three-Dimensional Free Vibration Analysis of Multi-Directional Functionally Graded Piezoelectric Annular Plates on Elastic Foundations via State Space Based Differential Quadrature Method. Appl Math Mech (2015) 36:439–64. 10.1007/s10483-015-1923-9
202.
Alibeigloo A . Static and Vibration Analysis of Axi-Symmetric Angle-Ply Laminated Cylindrical Shell Using State Space Differential Quadrature Method. Int J Press Vessels Piping (2009) 86(11):738–47. 10.1016/j.ijpvp.2009.07.002
203.
Ali MY Shankar K . Structural Health Monitoring of Composites Using System Identification. In: 15th Australian International Aerospace Congress (AIAC15); 25-28 February 2013; Melbourne, Australia (2013).
204.
Ali MY Shankar K . Agent Based Damaged Detection in Composite Laminates. Nondestructive Characterization Compos Mater Aerospace Eng Civil Infrastructure, Homeland Security (2013) 8694:528–33.
205.
Li D Qing GH . Free Vibration Analysis of Composite Laminates With Delamination Based on State Space Theory. Mech Adv Mater Structures (2014) 21(5):402–11. 10.1080/15376494.2012.697602
206.
Zhou Y Li S Zhou H . State Space Finite Element Analysis for Piezoelectric Precision Positioning Considering Secondary Converse Piezoelectric Effect. Finite Elem Anal Des (2015) 102:85–94. 10.1016/j.finel.2015.04.010
207.
Zhou Y Nyberg T Xiong G Li S . State Space Finite Element Analysis for Piezoelectric Laminated Curved Beam With Variable Curvature. Mech Adv Mater Structures (2020) 27(4):265–73. 10.1080/15376494.2018.1472323
208.
dos Santos CR Pacheco DR Taha HE Zakaria MY . Nonlinear Modeling of Electro-Aeroelastic Dynamics of Composite Beams With Piezoelectric Coupling. Compos Structures (2021) 255:112968. 10.1016/j.compstruct.2020.112968
209.
Sheng HY Ye JQ . A State Space Finite Element for Laminated Composite Plates. Comp Methods Appl Mech Eng (2002) 191(37-38):4259–76. 10.1016/s0045-7825(02)00379-1
210.
Zou GP Tang LM . A Semi-Analytical Solution for Laminated Composite Plates in Hamiltonian System. Comp Methods Appl Mech Eng (1995) 128(3-4):395–404. 10.1016/0045-7825(95)00877-2
211.
Zou GP Tang LM . A Semi-Analytical Solution for Thermal Stress Analysis of Laminated Composite Plates in the Hamiltonian System. Comput Structures (1995) 55(1):113–8.
212.
Sheng HY Ye JQ . A Semi-Analytical Finite Element for Laminated Composite Plates. Compos Structures (2002) 57(1-4):117–23. 10.1016/s0263-8223(02)00075-2
213.
Ye JQ Sheng HY Qin QH . A State Space Finite Element for Laminated Composites With Free Edges and Subjected to Transverse and In-Plane Loads. Comput Structures (2004) 82(15-16):1131–41. 10.1016/j.compstruc.2004.03.020
214.
Han ZL Cheng CZ Sheng HY . A State-Space Finite Element Method for Laminated Composite Plates Under Thermal Loading. J Therm Stresses (2017) 40(10):1285–302. 10.1080/01495739.2017.1319256
215.
Qing GH Qiu JJ Liu YH . Modified HR Mixed Variational Principle for Magnetoelectroelastic Bodies and State-Vector Equation. Appl Math Mech (2005) 26(6):722–8.
216.
Qing GH Qiu JJ Liu YH . A Semi-Analytical Solution for Static and Dynamic Analysis of Plates With Piezoelectric Patches. Int J Sol Structures (2006) 43(6):1388–403. 10.1016/j.ijsolstr.2005.03.048
217.
Qing GH Qiu JJ Liu YH . Free Vibration Analysis of Stiffened Laminated Plates. Int J Sol Structures (2006) 43(6):1357–71. 10.1016/j.ijsolstr.2005.03.012
218.
Liu YH Wang BH Qing GH . Free Vibration Analysis of Piezoelectric Laminated Plates With Delamination. Eng Mech (2012) 29(7):347–52.
219.
Zhou J Yang B . Three-Dimensional Analysis of Simply Supported Laminated Cylindrical Shells With Arbitrary Thickness. AIAA J (1996) 34(9):1960–4. 10.2514/3.13338
220.
Sheng HY Ye JQ . A Three-Dimensional State Space Finite Element Solution for Laminated Composite Cylindrical Shells. Comp Methods Appl Mech Eng (2003) 192(22-24):2441–59. 10.1016/s0045-7825(03)00265-2
221.
Qing GH Liu YH Qiu JJ Meng XJ . A Semi-Analytical Method for the Free Vibration Analysis of Thick Double-Shell Systems. Finite Elem Anal Des (2006) 42(10):837–45. 10.1016/j.finel.2006.01.002
222.
Jiang LZ Lee JS . Plane Orthotropic Layer by Transfer Matrix-Spline Boundary Element. J Eng Mech (1994) 120(5):1026–41. 10.1061/(asce)0733-9399(1994)120:5(1026)
223.
Ruddock GJ Spencer AJM . A New Approach to Stress Analysis of Anisotropic Laminated Elastic Cylinders. Proc R Soc Lond Ser A: Math Phys Eng Sci (1997) 453:1067–82. 10.1098/rspa.1997.0060
224.
Attallah KMZ Ye JQ Sheng HY . Three-Aimensional Finite Strip Analysis of Laminated Panels. Comput Structures (2007) 85(23-24):1769–81. 10.1016/j.compstruc.2007.04.003
225.
Khezri M Gharib M Bradford MA Vrcelj Z . Analysis of Thick and Orthotropic Rectangular Laminated Composite Plates Using a State-Space-Based Generalised RKP-FSM. Compos Structures (2015) 133:691–706. 10.1016/j.compstruct.2015.07.035
226.
Xin L Hu Z . Free Vibration of Layered Magneto-Electro-Elastic Beams by SS-DSC Approach. Compos Structures (2015) 125:96–103. 10.1016/j.compstruct.2015.01.048
227.
Chandrashekhara K Krishnamurthy K Roy S . Free Vibration of Composite Beams Including Rotary Inertia and Shear Deformation. Compos Structures (1990) 14(4):269–79. 10.1016/0263-8223(90)90010-c
228.
Rao MK Desai YM Chitnis MR . Free Vibrations of Laminated Beams Using Mixed Theory. Compos Structures (2001) 52(2):149–60.
229.
Fan JR . Exact Theory of Laminated Thick Plates and Shells. Beijing: Beijing Science (1996).
230.
Auricchio F Sacco E . A Mixed-Enhanced Finite-Element for the Analysis of Laminated Composite Plates. Int J Numer Methods Eng (1999) 44(10):1481–504. 10.1002/(sici)1097-0207(19990410)44:10<1481::aid-nme554>3.0.co;2-q
231.
Cheung YK . The Finite Strip Method in the Analysis of Elastic Plates With Two Opposite Simply Supported Ends. Proc Am Soc Civ Eng (1968) 94:1365–78.
232.
Fan SC Cheung YK . Static Analysis of Right Box Girder Bridges by Spline Finite Strip Method. Proc Inst Civil Eng (1983) 75(2):311–23. 10.1680/iicep.1983.1507
233.
Khezri M Vrcelj Z Bradford MA . Thin Plate Bending Analysis and Treatment of Material Discontinuities Using the Generalised RKP-FSM. Comp Model Eng Sci (Cmes) (2012) 87(4):271–305.
234.
Pao YH Keh DC Howard SM . Dynamic Response and Wave Propagation in Plane Trusses and Frames. AIAA J (1999) 37(5):594–603. 10.2514/2.778
235.
Pao YH Su XY Tian JY . Reverberation Matrix Method for Propagation of Sound in a Multilayered Liquid. J Sound Vibration (2000) 230(4):743–60. 10.1006/jsvi.1999.2675
236.
Pao YH Sun G . Dynamic Bending Strains in Planar Trusses With Pinned or Rigid Joints. J Eng Mech (2003) 129(3):324–32. 10.1061/(asce)0733-9399(2003)129:3(324)
237.
Pao YH Chen WQ Su XY . The Reverberation-Ray Matrix and Transfer Matrix Analyses of Unidirectional Wave Motion. Wave Motion (2007) 44(6):419–38. 10.1016/j.wavemoti.2007.02.004
238.
Wang L Rokhlin SI . Stable Reformulation of Transfer Matrix Method for Wave Propagation in Layered Anisotropic Media. Ultrasonics (2001) 39(6):413–24. 10.1016/s0041-624x(01)00082-8
239.
Zhao Z Wang B Qian Z Yong YK . A Novel Approach to Quantitative Predictions of High-Frequency Coupled Vibrations in Layered Piezoelectric Plates. Int J Eng Sci (2020) 157:103407. 10.1016/j.ijengsci.2020.103407
240.
Zhao Z Chen W . Investigation on High-Frequency and Mode-Coupling Vibrations in Thickness-Extensional Piezoelectric Thin-Film Resonators With Initial Stress. Appl Math Model (2022) 112:78–90. 10.1016/j.apm.2022.07.030
241.
Chen Y Wu B Su Y Chen W . Effects of Strain Stiffening and Electrostriction on Tunable Elastic Waves in Compressible Dielectric Elastomer Laminates. Int J Mech Sci (2020) 176:105572. 10.1016/j.ijmecsci.2020.105572
242.
Shmuel G Debotton G . Band-Gaps in Electrostatically Controlled Dielectric Laminates Subjected to Incremental Shear Motions. J Mech Phys Sol (2012) 60(11):1970–81. 10.1016/j.jmps.2012.05.006
243.
Zhao Z Zhu J Chen W . Size-Dependent Vibrations and Waves in Piezoelectric Nanostructures: A Literature Review. Int J Smart Nano Mater (2022) 13(3):391–431. 10.1080/19475411.2022.2091058
244.
Stan G Ciobanu CV Parthangal PM Cook RF . Diameter-Dependent Radial and Tangential Elastic Moduli of ZnO Nanowires. Nano Lett (2007) 7(12):3691–7. 10.1021/nl071986e
245.
Wang KF Wang BL Kitamura T . A Review on the Application of Modified Continuum Models in Modeling and Simulation of Nanostructures. Acta Mechanica Sinica (2016) 32:83–100. 10.1007/s10409-015-0508-4
Summary
Keywords
state-space approach, complex structure, aerospace, structural theory, mechanical behavior, analytical and numerical methods
Citation
Zhao Z, Shen X, Su Y and Chen W (2023) State-Space Approaches to Complex Structures in Aerospace. Aerosp. Res. Commun. 1:12394. doi: 10.3389/arc.2023.12394
Received
08 November 2023
Accepted
30 November 2023
Published
19 December 2023
Volume
1 - 2023
Updates
Copyright
© 2023 Zhao, Shen, Su and Chen.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Weiqiu Chen, chenwq@zju.edu.cn
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.