Enhancing Micro-Droplet Mixing in Microfluidic Systems Via Electrowetting-Induced Parametric Oscillations

In the context of space exploration, electrowetting-on-dielectric (EWOD) microfluidic systems hold substantial promise for enhancing in-situ analysis and experimentation, particularly given its potential for precise control of fluid dynamics in the microgravity environment. This study investigates the effects of electrowetting-induced parametric oscillations on mixing efficiency within coalesced micro-droplets in EWOD microfluidic devices using numerical simulations. The mechanism by which parametric oscillation affects the mixing process of micro-droplets in EWOD devices is unraveled, which is previously uninverstigated in the literature to the best of our knowledge. The simulations reveal that parametric oscillations significantly increase vorticity magnitude and shear rate around the droplet interface, leading to improved mixing compared to free oscillation. Notably, the study identifies fluctuations in the mixing index associated with the oscillation-induced shape changes of the droplets. These findings underscore the potential of parametric oscillation as a strategy for optimizing mixing in EWOD systems, with implications for the design of more efficient microfluidic devices.

Introduction

Microfluidic technology plays a pivotal role in space research, particularly with the use of lab-on-chip platforms for conducting astrobiological studies in the unique conditions of microgravity and radiation exposure [1], in addition to the diagnostic tools utilized for monitoring the health and living conditions of astronauts [2, 3]. Microfluidic platforms have demonstrated their potential in facilitating complex biological experiments performed in of the International Space Station (ISS) and CubeSat missions [4, 5], offering a compact and efficient means of conducting biomedical research in microgravity. The integration of microfluidic technology in proposed NASA and ESA missions, such as the “tissue chips” initiative [6–8] and the ESA-SPHEROIDS project [9, 10], exemplifies the progressive role of microfluidics in space biology, signaling a trend towards more advanced and integrated space research capabilities.

Electrowetting-on-dielectric (EWOD) constitutes an advanced technique in of digital microfluidics, enabling the precise manipulation of droplets with volumes ranging from picoliters to microliters [11] by modulating their wettability through the application of variable voltages, thereby facilitating the execution of complex laboratory procedures [12]. In year 2018, EWOD-based microfluidics has been used as electrowetting heat pipes on the ISS, and key microfluidic operations (droplet motion and splitting) are examined [13]. The findings indicate that electrowetting experiments are feasible in a space environment, suggesting that concerns pertaining to safety, reliability, and compactness can be effectively addressed [14].

On the other hand, due to the small size of micro-droplets and the limited diffusivity of most analytes and reagents within biochemical analysis systems, the majority of microfluidic species transport systems operate at low Reynolds numbers (characterizing laminar flow) and high Peclet numbers (indicating minimal diffusion) [15]. This combination renders mixing within micro-droplets a significant challenge and a critical issue in the field of microfluidics. Traditional methods for enhancing droplet mixing involve moving the coalesced droplet back and forth on a grid of electrodes, which oscillates the droplet to increase the interfacial area and promote diffusive processes [16–18]. Recently, a common approach to improve micro-droplet mixing in digital microfluidics is to generate oscillations within the combined droplet by applying AC voltage [19, 20]. Resonant droplet oscillation can be triggered by applying AC voltage in the EWOD microfluidics, which has been experimentally [19, 21–26] and numerically [27] proven as an effective approach to microfluid mixing. The shape oscillation brought about by the resonance mode can induces transient and chaotic convective vortices around the droplet, which greatly accelerates the mixing process [25, 28].

There are numerous studies on the oscillation of AC voltage-actuated droplets, but only a few testified to the oscillation’s applicability for mixing enhancement, and most of them are experiments [27]. Therefore, more numerical simulations are required to give detailed characteristics of the fluid flow by visualization of the internal flow within the droplet [29]. Based on the above analysis, this study presents a numerical examination of the influence of parametric oscillation on the mixing process of micro-droplets within digital microfluidic systems. The parametric oscillation is induced by the application of voltages with high amplitude and a driving frequency, $f_d$, which is roughly double the resonance frequency of the droplet, $f_n$. Throughout the parametric oscillation, the mixing index, $MI$, displays an oscillatory pattern over time. The mixing index fluctuation, denoted as $M{I}_{\mathit{osc}}$, is extracted and analyzed. Additionally, the fluid dynamics triggered by the parametric oscillation and its effects on mixing efficacy are scrutinized. Our findings elucidate the underlying mechanisms by which parametric oscillation enhances mixing in electrowetting-driven merged micro-droplets.

Methods

In this section, the electrowetting mechanism that drives the droplet motion in digital microfluidics is introduced. A droplet manipulation scheme where the droplets are merged, oscillated, and mixed is presented. Finally, numerical models and formulations are established.

Droplet Manipulation Schemes

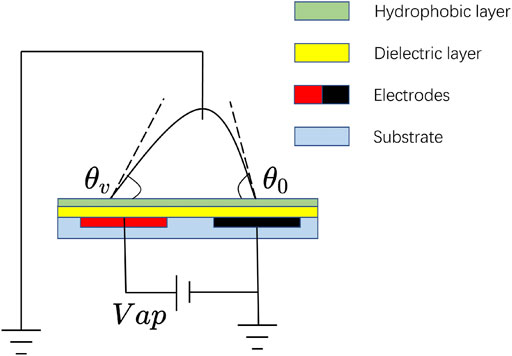
The manipulation of droplets in our study is based on the EWOD principle, as illustrated in Figure 1. The system comprises a dielectric layer, patterned electrodes, and a hydrophobic surface. A droplet, initially at rest with a contact angle ${\theta }_0$, is placed on this surface, bridging two electrodes. The application of a voltage $V_{ap}$ to an electrode induces electrowetting, reducing the contact angle to ${\theta }_v$ as described by the Young-Lippmann equation (Equation 1).

$\gamma \cos {\theta }_v-\gamma \cos {\theta }_0=\frac{1}{2}C{V}_{ap}^2(1)$

Figure 1

Figure 1. The schematic diagram of an open EWOD digital microfluidic system.

Where $\gamma$ represents the liquid-gas surface tension coefficient, $C$ denotes the dielectric layer’s capacitance per unit area. A pressure gradient induced by ${\theta }_v<{\theta }_0$ propels the droplet towards the right. EWOD effect enables droplet transport by altering the contact angle, with the driving frequency $f_d$ corresponding to half the frequency of the applied AC voltage, $f_{ac}$. Basic operations include transport, coalescence, division, and dispensing, typically managed through a two-dimensional electrode array [30]. Figure 2 outlines the electrode actuation scheme for droplet merging. Initially, droplets 1 and 2, with and without dye, respectively, are positioned at the interface of electrodes 1-2 and 3-4 [Figure 2A]. Activation of electrodes 2 and 3 at $t=0$ s induces electrowetting effect, causing the droplets to merge into droplet 3 [Figures 2B, C].

Figure 2

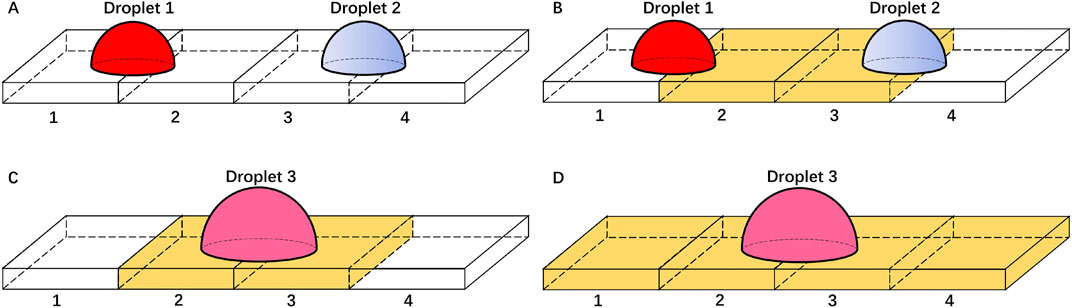
Figure 2. The electrode actuation scheme for droplet merging. Droplet 1 is filled with dye and droplet 2 is not. The voltages for the white electrode and the yellow electrode are 0 and $V_{ap}$, respectively. (A) initial state, (B) $t=0$, (C) droplet 1 and droplet 2 are merged into droplet 3, and (D) $t=t_{\mathit{merge1}}$, all the electrodes are on, and the droplet 3 oscillates freely.

Before applying AC voltage to the droplet, some prepatory work are done. At $t=t_{\mathit{merge1}}$, all the electrodes are activated to smear out the influence of electrode 1 and 4 on the merged droplet’s motion, as shown in Figure 2D. The droplet oscillates under a uniform electric field due to inertia. At $t=t_{\mathit{merge2}}$, the droplet has been fully merged and the natural oscillation amplitude has been dissipated a lot. At this time, apply AC voltage to all the electrodes. As a result, the contact angle $\theta$ constantly changes according to Equation 1, and the droplet mixes with oscillation. Scaled by the capillary timescale $t_c=\sqrt{\rho R_0^3\gamma }$, the two nondimensionalized critical time ${\bar{t}}_{\mathit{merge1}}$ and ${\bar{t}}_{\mathit{merge2}}$ are set as 2.05 and 24.81, respectively.

For the simulation, the electrowetting effect is modeled by periodically varying the contact angle according to Equation 2, where ${\theta }_{\mathit{max}}$ and ${\theta }_{\mathit{min}}$ represent the maximum and minimum contact angles, respectively.

$\theta =\frac{{\theta }_{\max }-{\theta }_{\min }}{2}\sin \left(2\pi f_{d}t-\frac{\pi }{2}\right)+\frac{{\theta }_{\max }+{\theta }_{\min }}{2},(2)$

This approach simplifies the numerical simulation by replacing the complex electrowetting dynamics with a sinusoidal variation of the contact angle [27, 31].

Numerical Modeling and Interface Tracking

The numerical modeling of the incompressible microfluidic flow in this study is based on the Navier-Stokes (NS) equations, which are given by Equation 3 for the momentum conservation and Equation 4 for the incompressibility condition.

$\rho \frac{\partial \vec{u}}{\partial t}+\rho \left(\vec{u}\cdot \nabla \right)\vec{u}=-\nabla p+\nabla \cdot \left[\mu \left(\nabla \vec{u}+{\left(\nabla \vec{u}\right)}^T\right)\right]+{\vec{F}}_{\text{st}}+\rho \vec{g}(3)$

$\nabla \vec{u}=0(4)$

Where $\rho$ is the density, $\vec{u}$ is the velocity, $p$ is the pressure, ${\vec{F}}_{st}$ is the surface tension, $\vec{g}$ is the gravitational acceleration, and $t$ is time. The water droplet dimensions are on millimeter scale, resulting in a Bond number, $Bo=\frac{\rho g{l}^2}{\gamma }$, less than unity, where $l$ is the droplet’s characteristic length scale. Thus, gravitational forces in Equation 3 are neglected [32].

The phase-field method is employed to track the dynamic interface of the droplet. The phase-field variable $\varphi$ and its chemical potential $G$ are introduced to replace the surface tension term ${\vec{F}}_{st}$ in Equation 3 with $G\nabla \varphi$, as shown in Equation 5. The Cahn-Hilliard equation governs the evolution of $\varphi$ and ensures that it assumes values of −1 or 1, except in a thin region at the fluid-fluid interface, as shown in Equation 6, where $\chi$ is the diffusion parameter, called the mobility:

${\vec{F}}_{st}=G\nabla \varphi (5)$

$\frac{\partial \varphi }{\partial t}+\vec{u}\cdot \nabla \varphi =\nabla \cdot \chi \nabla G(6)$

The mass equation, given by Equation 7, is used to calculate the dye concentration within the droplets, where $c$ is the concentration of the solute, $D_{ab}$ is the diffusivity, and $R$ is the reaction rate. The equation describes the transport of solute within the merged droplet, where the initial concentration in one droplet is $c_0$ and in the other is 0. The solute spreads until the concentration is uniform throughout the merged droplet. The reaction rate $R$ is set to 0 in this study.

$\frac{\partial c}{\partial t}-\nabla \cdot \left(D_{ab}\nabla c\right)+\vec{u}\cdot \nabla c=R(7)$

Computational Setup and Validation

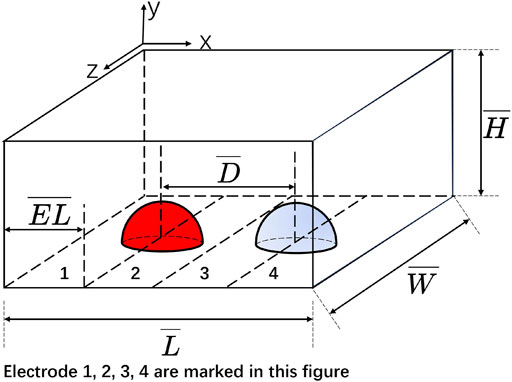
Figure 3 presents the schematic of the computational domain, where two identical droplets are centrally located on electrodes 1 and 2, and electrodes 3 and 4, respectively. The red and blue droplets refer to droplet with and without dye, respectively. The droplets consist of water, with their physical properties listed in Table 1. The initial droplets are hemispheres with a radius of $R_0$. The domain size is non-dimensionalized based on the initial droplet radius $R_0$, which serves as the reference length scale; the corresponding geometrical parameters are detailed in Table 2.

Figure 3

Figure 3. An illustration of the computational domain.

Table 1

Table 1. The physical properties of the droplet.

Table 2

Table 2. The nondimensional geometrical parameters of the computational domain.

Adaptive mesh refinement, known to optimize computational efficiency and accuracy for transient flows, is employed with a two-level approach. The simulation utilizes a uniform square mesh with a base grid spacing of $R_0$/5, determined by a grid refinement study. Near the droplet interface, the mesh is refined to 1/4 of the base grid spacing. Boundary conditions include a Navier slip at the domain bottom and no-slip conditions at the top and sides.

To ensure numerical stability across capillarity, viscosity, and Courant criteria, the time step is dynamically adjusted [33]. Mesh independence is confirmed by simulating with mesh sizes of $R_0/16$, $R_0/20$, and $R_0/25$ near the interface for 0˜0.009 s for Case R1.12-60-90. Detailed mesh independence study can be found in our previous work [27]. Finally, a mesh size of $R_0=20$ near the interface is chosen and implemented in all the simulations.

Results and Discussion

This study mainly focuses on the oscillation of the merged droplet. Hence, the simulated merging process is not presented. The onset of parametric instability within the droplet initiates lateral and vertical wave formation, leading to a star-shaped oscillatory pattern and surface undulations. This phenomenon has been investigated in several researches [34–39]. Research on initiating parametric oscillations within micro-droplets in electrowetting-on-dielectric (EWOD) microfluidic systems has been documented in the literature [24, 40]. Bansal et al. have induced parametric oscillation in coalesced droplets, which markedly enhances the mixing efficiency and slashes the diffusive mixing time by as much as 98% [24]. The oscillatory behavior of the droplet’s shape gives rise to distinct flow patterns, which merit further elaboration. The flow dynamics are examined numerically and compared with existing literature to ascertain the accuracy of the findings. Furthermore, the study presents and contrasts the vortices and shear rate distributions in the presence and absence of oscillations, thereby elucidating the flow dynamics induced by electrowetting-driven oscillations.

Multiple cases are studied to ensure the validity of our results. The cases studied here are listed in Table 3 and referred to by their names in the following paragraphs for simplicity. The name of the case refers to its initial radius of the two droplets $R_0$, maximum contact angle ${\theta }_{\mathit{max}}$, and minimum contact angle ${\theta }_{\mathit{min}}$.

Table 3

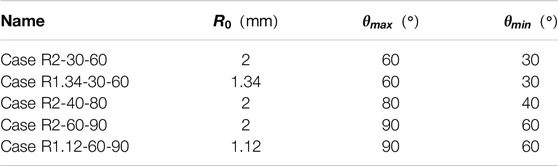
Table 3. The cases used in the study. The name of the case refers to its initial radius of the two droplets $R_0$, maximum contact angle ${\theta }_{\mathit{max}}$, and minimum contact angle ${\theta }_{\mathit{min}}$.

To enhance clarity in the presentation of results, certain data have been rendered dimensionless. This normalization can be discerned by noting the presence of horizontal lines above the respective data headers, for example, $\bar{x}$ represents the scaled horizontal coordinate. Unless otherwise specified, length-related parameters are scaled using $R_0$, time parameters are scaled using the capillary timescale $t_c=\sqrt{\rho R_0^3\gamma }$, and frequency-related parameters are scaled using $1/t_c$.

Parametric Oscillation

By subjecting the droplet to a driving frequency $f_d$ that is twice its resonance frequency $f_n$ under enough amplitude, parametric instability can be triggered in droplet. The oscillation mode number is marked as $n$. One characteristic of the parametric instability is the periodic lateral wave that appear in the azimuthal direction of the droplet. Figure 4F is a bottom view of the droplet, where the droplet radius $R_b$ can be regarded as a superposition of the equatorial radius $R_a$ and the lateral disturbance ${\eta }_{\text{xz}}$.

Figure 4

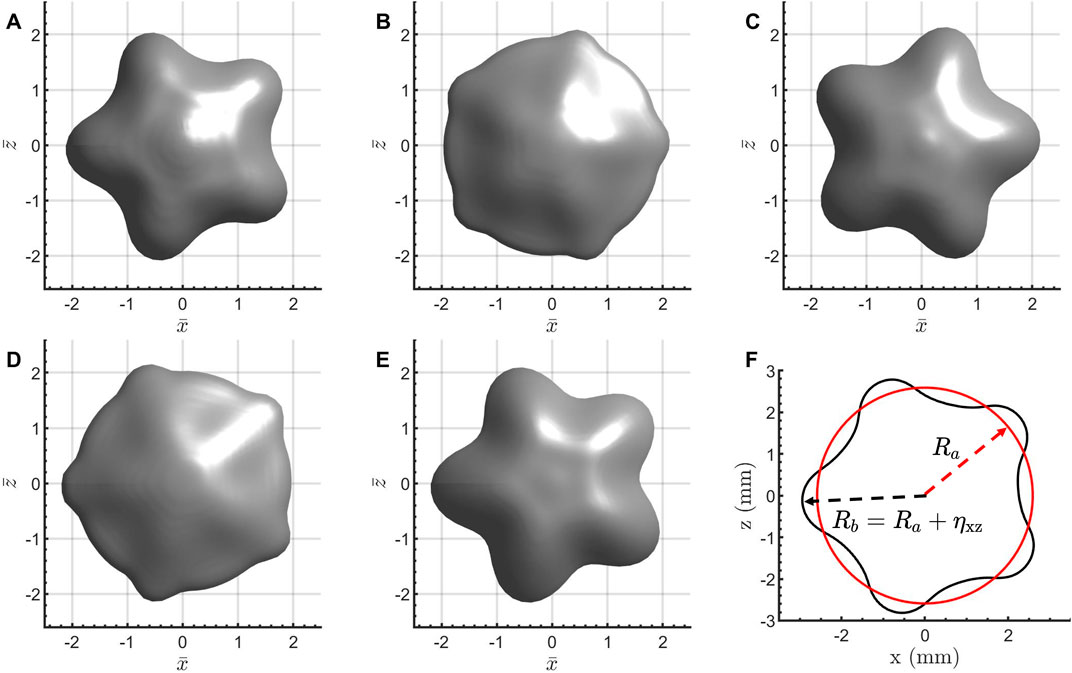
Figure 4. A cycle of the parametrically oscillating droplet at $n=5$ mode, taking Case R1.34-30-60, $n=5$ mode as an example. The phase of each droplet in a cycle is: (A) $T$, (B) $T/4$, (C) $T/2$, (D) $3T/4$, (E) $T$, where $T$ refers to a period of the droplet oscillation. (F) is the bottom view of the droplet, showing that the droplet radius R_b can be decomposed into R_a and η_xz.

The theoretical resonance frequency of the sessile droplet can be estimated according to Equations 8, 9:

${\omega }_n=\beta \sqrt{\frac{n\left(n-1\right)\left(n+2\right)\gamma }{\rho R_a^3}}(8)$

$f_n=\frac{{\omega }_n}{2\pi }(9)$

Where ${\omega }_n$ is the angular resonance frequency, $\gamma$ is the surface tension coefficient, $\rho$ is the density of the droplet, $R_a$ is the time-varying equatorial radius, $n$ is the mode number, and $\beta$ is the modification parameter, which ranges from 0.7 to 1 in our study. The mode number $n$ also implicates the number of lobes that appears in the star-shaped droplet. Up to eight modes of parametric oscillations are founded in this study.

The temporal evolution of the lateral wave is depicted in Figure 4, aligning closely with previously published findings [37, 38]. The oscillation period is identified as $T$. The moment at which the droplet achieves its most star-like form is designated as $t_{\text{star}}$ and is considered the onset of the cycle, as illustrated in Figure 4A. Subsequently, the star-shaped droplet initiates the process of contracting its elongated lobes while elongating its shorter lobes. Over time, the droplet’s base transforms into a spherical shape, with the lateral wave reaching zero amplitude, as shown in Figure 4B at $T/4$. The previous short and long lobes continue their respective processes of elongation and contraction, culminating in a star droplet that is the inverse of its initial state, as depicted in Figure 4C. For the sake of clarity, the initial star droplet configuration is referred to as ${\text{star}}^{+}$, while the droplet’s configuration at $T/2$ is designated as ${\text{star}}^{-}$. Between $T/2$ and $T$, the droplet undergoes a symmetrical shape transformation, ultimately reverting to the ${\text{star}}^{+}$ configuration, as shown in Figures 4D, E.

Calculation of the Most Star-Like Moment for Droplet

The instant at which the droplet reaches its most pronounced star-shaped form is denoted as $t_{\text{star}}$, serving as a reference for identifying the full oscillation cycle of the star-shaped droplet. As the droplet undergoes continuous changes in its equatorial radius $R_a$, a modified measure of standard deviation, denoted $\bar{\sigma }(t)$, is proposed for the determination of $t_{\text{star}}$, as outlined in Equation 10. Here, the standard deviation $\sigma (t)$ is normalized by the equatorial radius $R_a(t)$. This normalization serves to remove the variability caused by the changing $R_a(t)$. The adjusted standard deviation $\bar{\sigma }(t)$ quantifies the deviation of the droplet from a spherical shape, with $t_{\text{star}}$ corresponding to the peak value of $\bar{\sigma }(t)$. To calculate $\bar{\sigma }(t)$, data from the droplet’s stable oscillatory state are utilized, with $t_{\text{star}}$ is identified at the points of local maxima.

$\bar{\sigma }\left(t\right)=\frac{1}{R_a\left(t\right)}\sqrt{\frac{{\sum }_{i=1}^N{\left(R_{b,i}\left(t\right)-R_a\left(t\right)\right)}^2}{N}}(10)$

Flow Analysis

The parametric oscillation brings about not only shape changes, but also characteristic internal flow patterns, which will be discussed in the following paragraphs.

Validation

The internal flow in parametrically oscillating star-shaped droplet can be assumed as potential flow [41]. The radial internal flow velocity $v_r$ in the bottom of the droplet can be expressed as follows:

$v_r=-V_n{\left(\frac{r}{R_a}\right)}^{n-1}\cos \left(n\phi \right)\sin \left({\omega }_{n}t\right),(11)$

In Equation 11, $V_n$ represents the peak fluid velocity observed at the equatorial periphery as the droplet returns to its equilibrium form. Additionally, $r$ denotes the radial distance from the droplet’s center, while $\phi$ specifies the azimuthal angle.

The distribution of the radial velocity $v_r$ at the base of the droplet is illustrated in Figure 5A. Here, the droplet is in the $T/4$ phase, and the radial velocity exhibits a sinusoidal pattern around its circumference, characterized by the presence of eight wave crests. Figure 5B depicts the variation of the measured radial velocity $v_r$ as a function of the azimuthal angle. The sinusoidal nature of the curve and the number of crests are in excellent agreement with the predictions of Equation 11, confirming that the flow dynamics observed in this study are consistent with the potential flow theory proposed in the literature [41] for parametric oscillations of droplets. The streamlines at the bottom of the droplet for Case R2-60-90, with a driving frequency of $f_d=55$ Hz and at the $n=2$ mode, are presented in Figure 6. This figure reveals a strong correlation with the experimental particle trace observations reported in the literature [41] for droplets undergoing parametric oscillations at the $n=2$ mode.

Figure 5

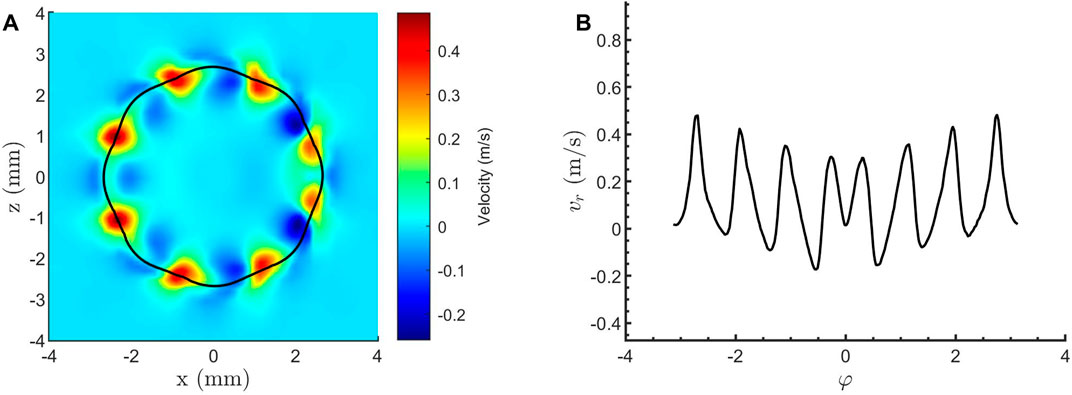
Figure 5. Radial velocity $v_r$ distributions for a droplet oscillating in the $n=8$ mode at the $T/4$ phase for Case R1.34-30-60 with a driving frequency of $f_d=375$ Hz. (A) Radial velocity distribution at the droplet’s base. (B) Radial velocity at the droplet’s equatorial edge.

Figure 6

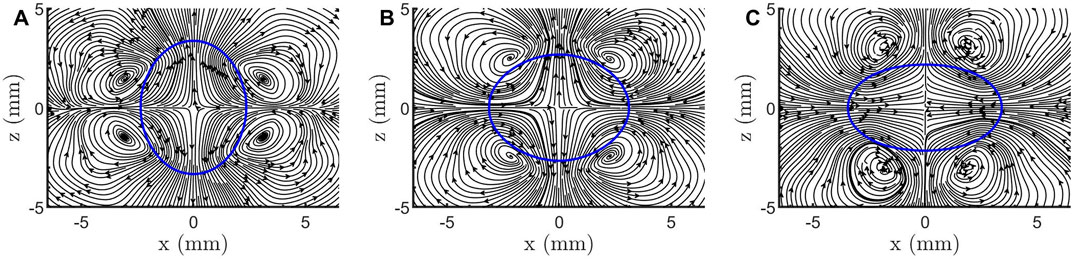
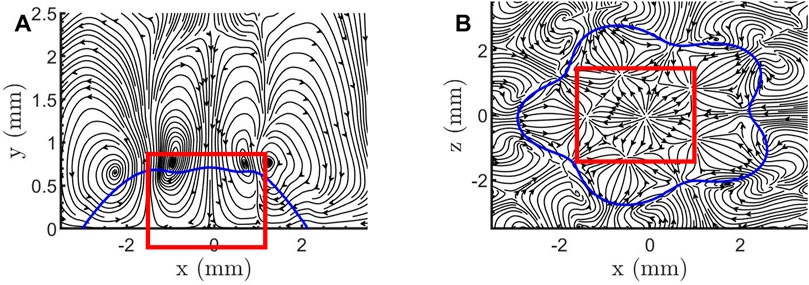
Figure 6. Streamline patterns at the base of the droplet for Case R2-60-90 in the $n=2$ mode at a driving frequency of $f_d=55$ Hz. The depicted phases of the droplet within its oscillation cycle are: (A) $T/8$, (B) $T/4$, and (C) $3T/8$, with $T$ denoting the oscillation period of the droplet.

Vortex and Shear Rate Analysis

The internal flow in the droplet includes flows in two directions, the up-down direction and the azimuthal direction, which can be seen by the streamlines in the x-y plane and x-z plane, respectively. The streamlines radiating from the center in Figure 7B correspond to the droplet’s flow at the bottom center reflected in Figure 7A. Therefore, this part of the streamlines in Figure 7B is not connected to the streamlines at the edge of the droplet, exhibiting a discontinuous pattern.

Figure 7

Figure 7. Streamlines in Case R1.34-30-60, $n=5$ mode, for (A) x-y plane, (B) x-z plane.

Cases excited with parametric oscillation show higher vorticity magnitude and shear rate than cases with no actuated oscillation and no parametric oscillation, as shown in Figure 8. Case R2-40-80 display $n=5$ mode parametric oscillation at $f_d=165$ Hz, and display no parametric oscillation mode at $f_d=175$ Hz, whose driving frequency is close to $f_d=165$ Hz. The former case shows stronger vorticity and shear rate than the later in the liquid-gas interface of the droplet [Figures 8A, C, D, F]. This may due to the higher oscillation amplitude brought about by the resonance mode, which also explains why Case R2-40-80 show higher vorticity and shear rate than cases with no actuated oscillation [Figures 8A, B, D, E].

Figure 8

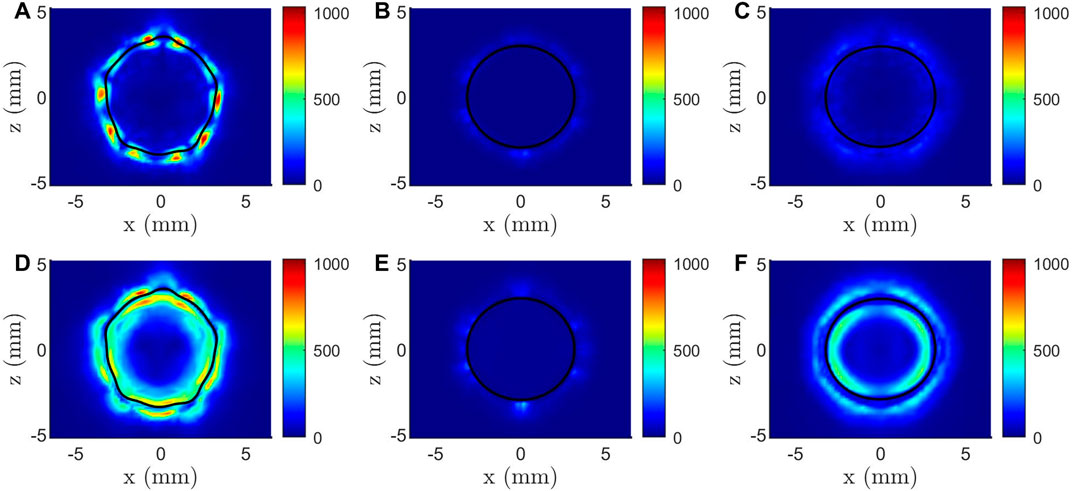
Figure 8. Vorticity magnitude (top row) and shear rate (bottom row) distributions at the droplet’s base for different experimental conditions. (A, D) Case R2-40-80 with $n=5$ mode excited at $f_d=165$ Hz; (B, E) Case R2 of free oscillation; (C, F) Case R2-40-80 with no parametric oscillation mode, excited at $f_d=175$ Hz.

Also, the distribution of the vortices and shear rate is worth studying. The vortices rarely appears inside the droplet, owing to the laminar nature of the micro-droplet. Nevertheless, there are still strong vortices near the liquid-gas interface of the droplet, most of which are distributed around the intersections of its lobes. This rule applies to all parametric oscillation cases studied here, as shown in Figures 9A∼F. In the bottom plate, the temporal change of contact angle result in intense velocity gradient in the liquid air interface, [Figure 5] which may cause rotations of the fluid microelements and generate vortices around the liquid-gas interface. Considering $t=T/4$ to $T/2$ when the previous short and long lobes continue their respective processes of elongation and contraction [Figures 4B, C], the velocity directions of two adjacent lobes are opposite to each other. Therefore, the velocity gradient at the intersection of two adjacent lobes is the greatest, which explains why the vorticity magnitude is mainly concentrated at these intersections. The shear rate are mainly located near and inside the liquid-gas interface [Figures 10A∼F]. This can also be explained by the extension and retraction of the droplet brought about by the parametric oscillation. Due to the change in the curvature of the droplet, the interfacial tension generates an inward or outward pressure, resulting in stronger shear rate within the droplet.

Figure 9

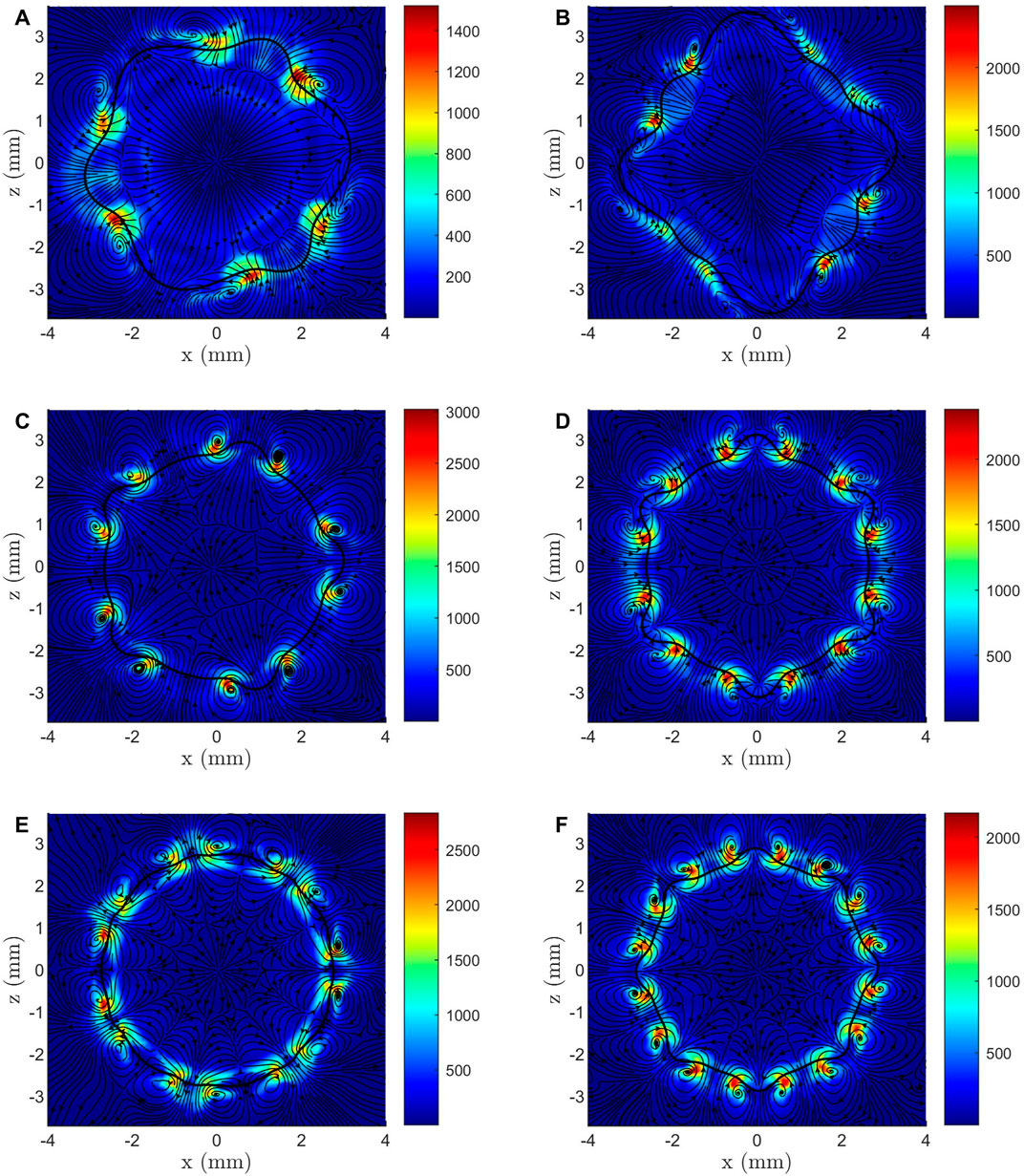
Figure 9. Vorticity magnitude distribution in Case R1.34-30-60 for (A) $n=3$ mode, (B) $n=4$ mode, (C) $n=5$ mode, (D) $n=6$ mode, (E) $n=7$ mode, (F) $n=8$ mode.

Figure 10

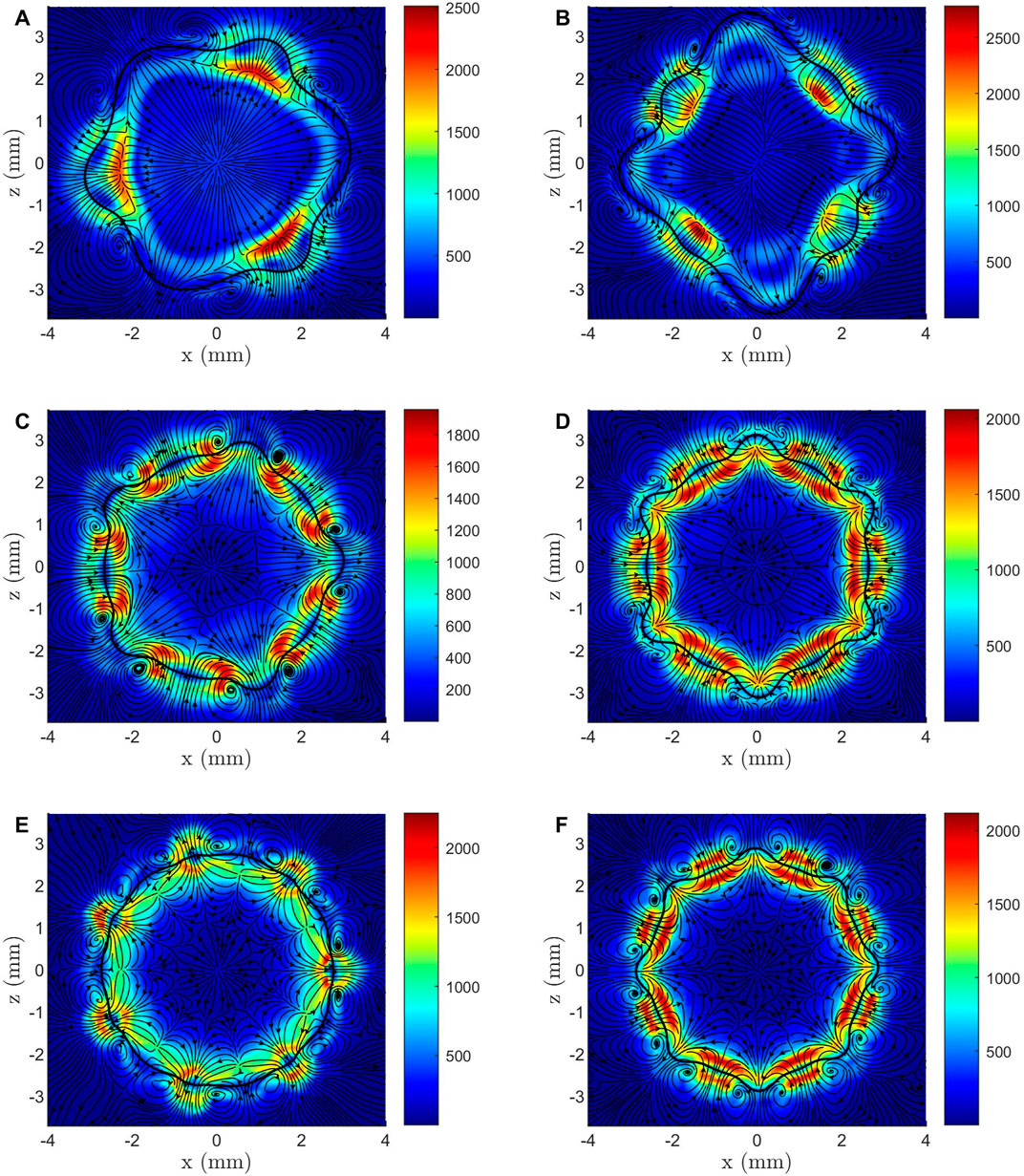
Figure 10. Shear rate magnitude distribution in Case R1.34-30-60 for (A) $n=3$ mode, (B) $n=4$ mode, (C) $n=5$ mode, (D) $n=6$ mode, (E) $n=7$ mode, (F) $n=8$ mode.

The Mixing Process

In this section, the impact of the parametric oscillation on the mixing process is analyzed. We studied the dye distribution in droplets and defined the mixing index $MI$ by scaling the variance ${\sigma }_c^2$ of the chemical concentrations in the transient regime [27, 42] as shown in Equations 12, 13:

${\sigma }_c^2≔\frac{1}{N_{\text{tot}}}{\oint }_V{\left(c\left(x,y,z,t\right)-\bar{c}\left(t\right)\right)}^2\mathrm{d}V,(12)$

$MI≔1-\frac{{\sigma }_c^2}{\bar{c}},(13)$

Where $N_{\text{vol}}(t)≔{\oint }_{V}c(x,y,z,t)\mathrm{d}V$ corresponds to the amounts of molecules in the volume, and $\bar{c}$ is the mean concentration. The mixing index $MI$ ranging from 0 to 1 represents the mixing efficiency, and reaches 1 when the dye in the droplet is fully mixed.

Mixing Enhancement Achieved by Parametric Oscillation

At $\bar{t}=45.71$, the droplet is almost mixed for Case R2-30-60 and Case R1.34-30-60, and the corresponding mixing index is marked as $M{I}_{45.71}$. Cases where droplet is not applied with AC voltage and oscillates freely are denoted as free oscillation. The mixing efficiency of the AC voltage-actuated oscillation cases and the free oscillation cases are compared by checking their mixing index $MI$ at $\bar{t}=45.71$, as shown in Figure 11. The cases with AC voltage-actuated oscillation show better mixing efficiency than the cases of free oscillation, which is in good agreement with previous numerical and experimental studies [19, 21, 24, 27]. Hence, the parametric oscillation actuated by the AC voltage can be applied to enhance mixing in micro-droplet. It has been mentioned in Vortex and Shear Rate Analysis that the vorticity magnitude and shear rate in parametric oscillation cases are higher than that in free oscillation cases. The vortices mainly distribute around the liquid-gas interface of the droplet, accelerating the mass transfer near the interface, and hence attribute to the overall increase of the mixing index. The shear rate distributed near and inside the liquid-gas interface can lead to the stretching and compression of fluid micro-elements, thereby disrupting the laminar structure within the fluid and promoting the mixing between different components. In summary, compared to free oscillation cases, parametric oscillation brings about higher vorticity magnitude and shear rate near the droplet liquid-gas interface, which enhances the mixing efficiency.

Figure 11

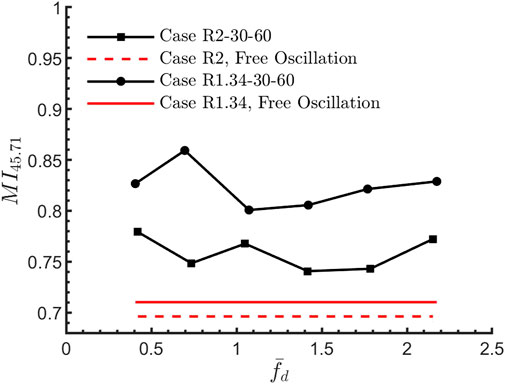
Figure 11. The mixing index $MI$ at $\bar{t}=45.71$ for Case R2-30-60, Case R1.34-30-60, and their corresponding free oscillation cases. Free oscillation refers to the cases where the droplet is not applied with AC voltage and oscillates freely.

The Mixing Index Fluctuation

Besides the mixing enhancement, the parametric oscillation also introduces fluctuations in the mixing index $MI$ curve, as shown in Figure 12A. The $n=2$ parametric mode is excited at ${\bar{f}}_d=0.58$ for Case R2-60-90, which are denoted as resonance in Figure 12A. The parametric mode case show fluctuation in the $MI$ curve, while the free oscillation and no resonance cases do not. This rule applies to all cases computed in this study. The original $MI$ curve was processed to obtain a smoothed version using the locally weighted scatter plot smooth method implemented in MATLAB. This smoothing procedure allowed for the extraction of the fluctuation patterns from the original $MI$ curve, thereby providing a method to quantify the fluctuations introduced by the parametric oscillation. The fluctuations in $MI$ curve are referred to as $M{I}_{\mathit{osc}}$ in the following text.

Figure 12

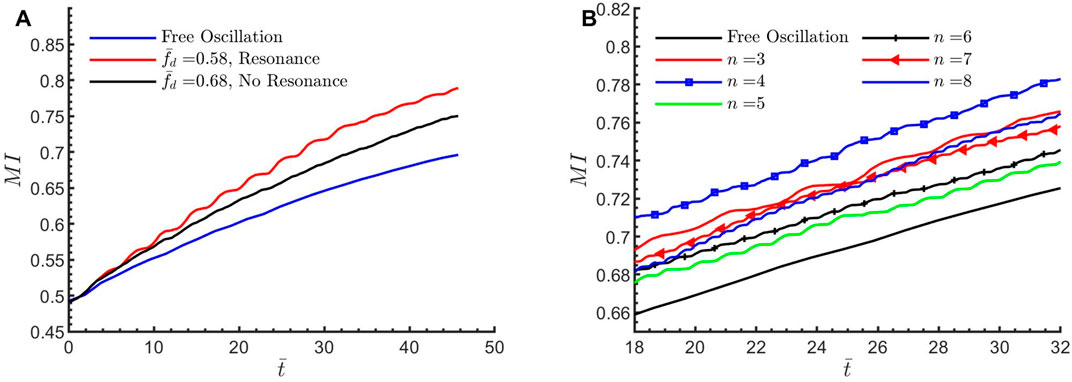
Figure 12. Time variation of the mixing index $MI$ for (A) the free oscillation case, the resonance condition with ${\bar{f}}_d=0.58$, and the non-resonance condition with ${\bar{f}}_d=0.68$. [Case R2-60-90] (B) Case R1.34-30-60 and its corresponding free oscillation case. Note that the presence of parametric oscillation is observed to cause fluctuations in the $MI$ curve.

The mixing index $MI$ curves for Case R1.34-30-60 and its corresponding free oscillation case are plotted in Figure 12B. Except the free oscillation case, all parametric oscillation cases show apparent mixing index fluctuations $M{I}_{\mathit{osc}}$. Applying FFT (Fast-Fourier Transformation) to the mixing index fluctuation $M{I}_{\mathit{osc}}$, the main fluctuating frequency of $M{I}_{\mathit{osc}}$ show good agreement with its driving frequency ${\bar{f}}_d$, as shown in Figure 13. This finding also validate that the mixing index fluctuation is introduced by the parametric oscillation. The mechanism of how parametric oscillation brings about this mixing index fluctuation $M{I}_{\mathit{osc}}$ is demonstrated by analyzing the dye distribution of the droplet. The dye distribution for Case R1.34-30-60, $n=5$ mode is plotted in Figure 14, with positions of four dye lobes marked from 1 to 4 for further discussion. Dye lobes refer to the lobe shape that appear in the dye distribution, which is different from the lobes used when describing the shape of the star-shaped droplet. Between $T/4$ and $T/2$, the droplet undergoes a transformation from a spherical to a ${\text{star}}^{+}$ configuration (Figures 14A–C). This morphological transition leads to the progressive convergence of dye lobes 2 and 3, which are increasingly compressed and eventually coalesce into a unified lobe, as depicted in Figure 14C. Subsequently, during the interval from $3T/4$ to $T$, the droplet shifts from a spherical to a ${\text{star}}^{-}$ shape (Figures 14D–F). In a similar manner, dye lobes 1 and 2 merge into one lobe, while dye lobes 3 and 4 amalgamate into a separate lobe, as illustrated in Figure 14F. According to these procedures, the mixing index may reach local maximum at $T/2$ or $T$ since some dyes are compressed into one lobe, which explains the origin of the mixing index fluctuation $M{I}_{\mathit{osc}}$. The intimate relationship between $M{I}_{\mathit{osc}}$ and the droplet’s shape transformation suggests that the primary oscillation frequency of $M{I}_{\mathit{osc}}$ should be twice that of the parametric oscillation frequency, $f_{\mathit{osc}}$, which is equivalent to the driving frequency, $f_d$. This frequency prediction aligns with the Fast Fourier Transform (FFT) results presented in Figure 13. The moment of the most star-like moment, $t_{\mathit{star}}$, should also corresponds to the local peak of the mixing index, or the crest of $M{I}_{\mathit{osc}}$. This is confirmed by Figure 15. Therefore, the proposed mechanism, whereby parametric oscillation induces $M{I}_{\mathit{osc}}$ fluctuations by consolidating dye lobes into a unified shape, is consistent with the FFT characteristics and the correspondence of the $M{I}_{\mathit{osc}}$ curve peaks to $t_{\text{star}}$.

Figure 13

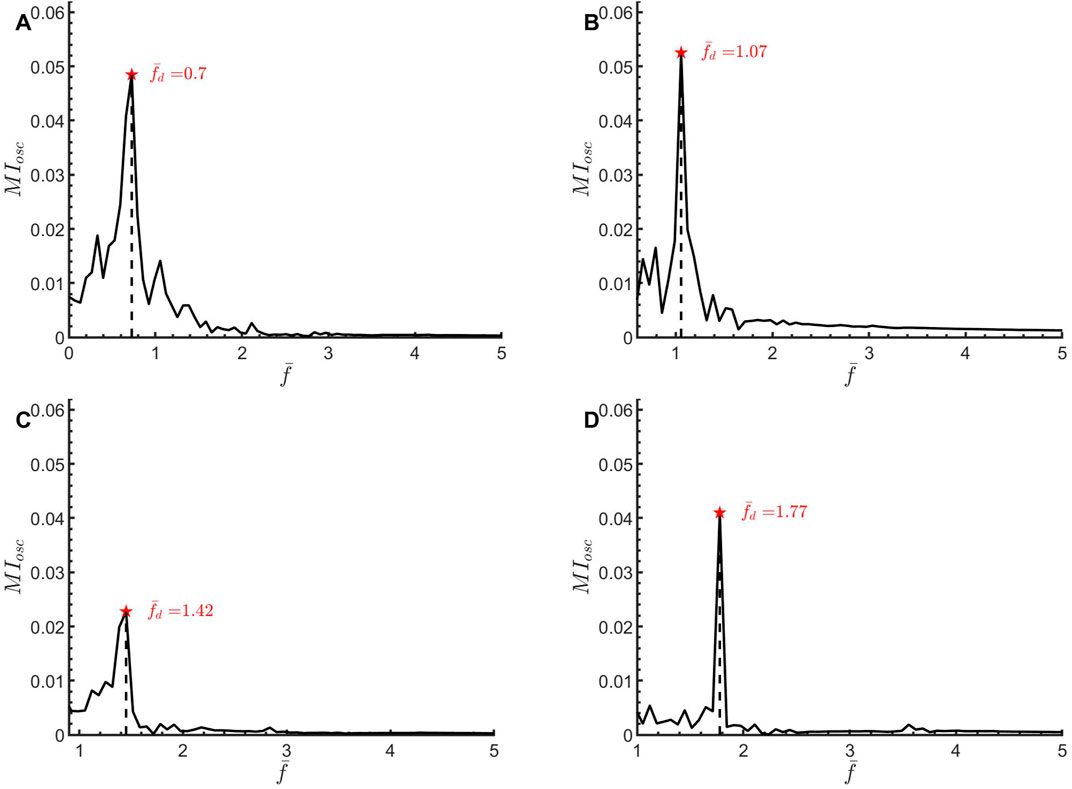
Figure 13. Fast Fourier transform of the mixing index fluctuation $M{I}_{\mathit{osc}}$ in Case R1.34-30-60, for (A) $n=4$ mode, ${\bar{f}}_d=0.7$ (B) $n=5$ mode, ${\bar{f}}_d=1.07$ (C) $n=6$ mode, ${\bar{f}}_d=1.42$ (D) $n=7$ mode, ${\bar{f}}_d=1.77$.

Figure 14

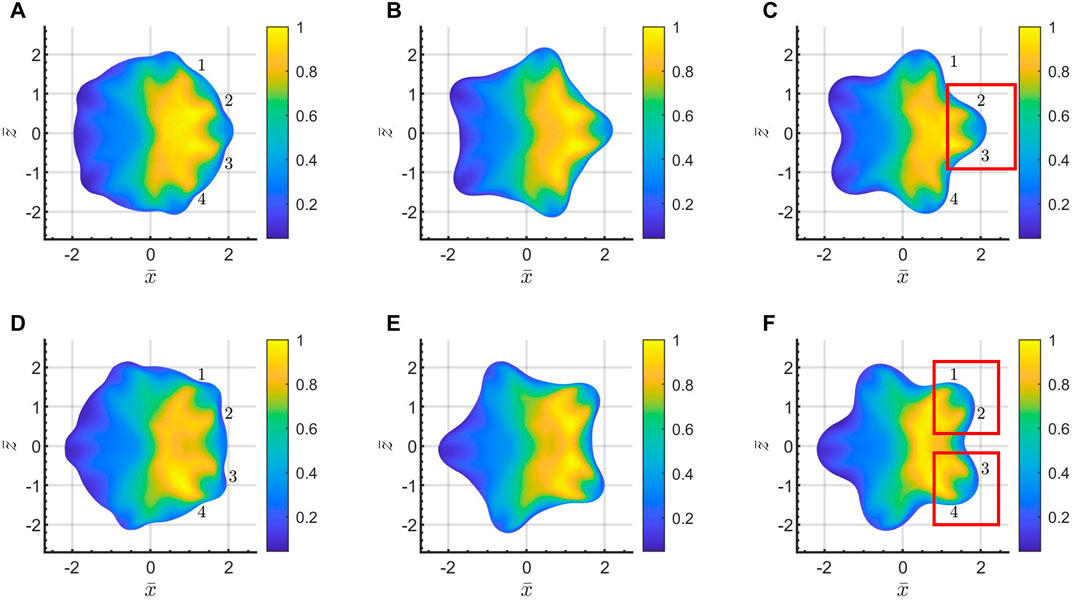
Figure 14. Distribution of the dye concentration for Case R1.34-30-60, $n=5$ mode. For better illustration, the spatiotemporal concentration $c(x,z,t)$ is normalized by the transient maximum concentration $c_{\mathit{max}}(t)$ in this figure. Positions for four dye lobes are marked as 1 to 4 for further discussion. (A) $t=T/4$, (B) $t=3T/8$, (C) $t=T/2$, (D) $t=3T/4$, (E) $t=7T/8$, (F) $t=T$.

Figure 15

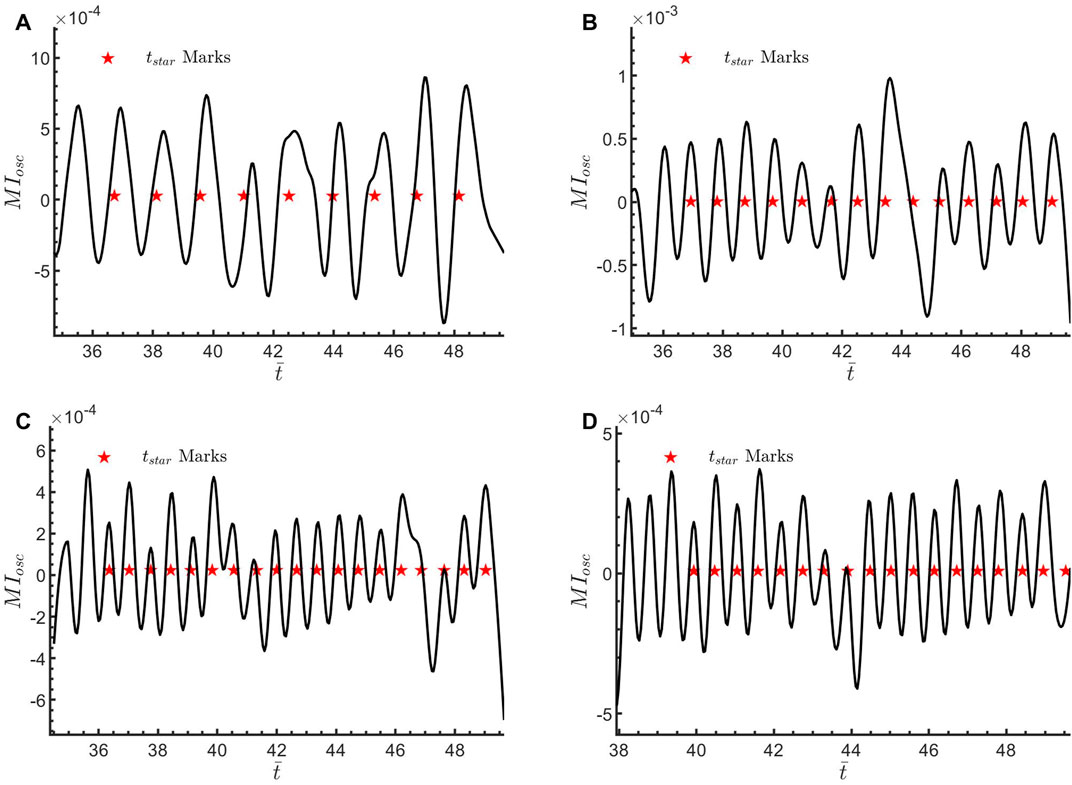
Figure 15. The time variation of the mixing index fluctuation $M{I}_{\mathit{osc}}$ for Case R1.34-30-60: (A) $n=4$ mode, (B) $n=5$ mode, (C) $n=6$ mode, (D) $n=7$ mode. The horizontal coordinates of the star marks correspond to the dimensionless value of the most star-like moment. For a more intuitive representation, the vertical coordinates of the star marks are set as the average of the values from the $M{I}_{\mathit{osc}}$ curve.

Conclusion

This study utilizes numerical simulations to investigate how electrowetting-induced parametric oscillations enhance mixing within a merged micro-droplet in Electrowetting-on-Dielectric (EWOD) microfluidic systems. It replicates a realistic scenario in EWOD digital microfluidics, where two micro-droplets collide head-on and merge, after which an AC voltage is applied to induce oscillations that improve mixing efficiency [15]. These parametric oscillations are intentionally triggered at specific frequencies and amplitudes. One of the droplets contains dye, allowing the mixing process to be meticulously examined through the distribution of dye concentration. The objective of this work is to numerically explore the mechanism by which parametric oscillation affects the mixing process of micro-droplets in EWOD devices, an area previously uninvestigated in the literature to the best of our knowledge. The following conclusions are drawn from the results presented:

First, the presence of parametric oscillation significantly influences the distribution and intensity of vortices and shear rate within the droplet flow field. The internal flow of the droplet exhibits directional characteristics in both the up-down and azimuthal directions. Parametric oscillation, particularly in resonance mode, enhances vorticity magnitude and shear rate at the liquid-gas interface compared to cases without actuated oscillation. Vortices are predominantly concentrated near the intersections of the droplet’s lobes, with minimal appearance inside the droplet due to its laminar nature. The shear rate are primarily localized near and inside the liquid-gas interface, influenced by the droplet’s extension and retraction caused by parametric oscillation.

Second, parametric oscillation is proven as an effective method for enhancing mixing in micro-droplets compared to free oscillation. At $\bar{t}=45.71$, droplets under AC voltage-actuated oscillation, particularly in Cases R2-30-60 and R1.34-30-60, exhibit near-complete mixing, as indicated by the mixing index $M{I}_{45.71}$. This is in contrast to free oscillation cases where no AC voltage is applied. The heightened vorticity and shear rate near the liquid-gas interface, a result of parametric oscillation, are key factors contributing to the enhanced mixing. Vortices near the interface accelerate mass transfer, while shear rate disrupt the fluid’s laminar structure, promoting inter-component mixing.

Finally, it is highlighted that parametric oscillation not only enhances mixing but also introduces significant fluctuations in the mixing index $(MI)$ curve. These fluctuations, termed $M{I}_{\mathit{osc}}$, are evident in all parametric oscillation cases studied, invisible for free oscillation and no parametric oscillation cases. The smoothed $MI$ curves, obtained through the locally weighted scatter plot smooth method, reveal the fluctuation patterns induced by parametric oscillation. The main fluctuating frequency of $M{I}_{\mathit{osc}}$ aligns with the driving frequency $\bar{f}d$, confirming the role of parametric oscillation in generating these fluctuations. The mechanism behind $MIosc$ is explained through the analysis of dye distribution within the droplet, showing how the droplet’s shape transformation from spherical to star-shaped configurations leads to the convergence and coalescence of dye lobes, resulting in local maxima of the mixing index. The frequency of $M{I}_{\mathit{osc}}$ is predicted to be twice that of the parametric oscillation frequency, which is consistent with FFT results and the correlation between the peaks of $M{I}_{\mathit{osc}}$ and the most star-like moment $(t_{\mathit{star}})$. This proposed mechanism provides a comprehensive understanding of how parametric oscillation influences the mixing process in droplets.

Ultimately, this research underscores the potential of parametric oscillation as a powerful tool for enhancing mixing in micro-droplets within EWOD systems. The detailed insights into the mechanisms behind mixing index fluctuations provide a novel understanding of droplet mixing dynamics, which can be directly applied to improve the design and operation of microfluidic devices for applications requiring efficient and controlled mixing processes.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

The first author, YW, conceptualization, methodology, numerical computation, and draft writing. The second author, JZ, funding acquisition, project administration, supervision, and draft reviewer. The third author, ZZ, investigation and methodology. The fourth author, JS, investigation and methodology. All authors contributed to the article and approved the submitted version.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors acknowledge financial support from the National Natural Science Foundation of China (Grant No. 12172329) and the National Science and Technology Major Project (Nos J2019-III-0004-0047 and 2019-III-0014-0058).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI Statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

References

1. Krakos, A. Lab-on-chip Technologies for Space Research — Current Trends and Prospects. Microchim Acta (2024) 191:31–21. doi:10.1007/s00604-023-06084-4

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Snyder, JE, Walsh, D, Carr, PA, and Rothschild, LJ. A Makerspace for Life Support Systems in Space. Trends Biotechnol (2019) 37:1164–74. doi:10.1016/j.tibtech.2019.05.003

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zangheri, M, Mirasoli, M, Guardigli, M, Di Nardo, F, Anfossi, L, Baggiani, C, et al. Chemiluminescence-based Biosensor for Monitoring Astronauts’ Health Status during Space Missions: Results from the International Space Station. Biosens Bioelectron (2019) 129:260–8. doi:10.1016/j.bios.2018.09.059

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Medha, M, and Roy, A. Microgravity: New Aspect for Breast Cancer Treatment, a Review. Acta Astronaut. (2022) 190:62–73. doi:10.1016/j.actaastro.2021.09.045

CrossRef Full Text | Google Scholar

5. Grimm, D, Schulz, H, Krüger, M, Cortés-Sánchez, JL, Egli, M, Kraus, A, et al. The Fight against Cancer by Microgravity: The Multicellular Spheroid as a Metastasis Model. Int J Mol Sci (2022) 23:3073. doi:10.3390/ijms23063073

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Mu, X, He, W, Rivera, VAM, De Alba, RAD, Newman, DJ, and Zhang, YS. Small Tissue Chips with Big Opportunities for Space Medicine. Life Sci Space Res (2022) 35:150–7. doi:10.1016/j.lssr.2022.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yau, A, Wang, Z, Ponthempilly, N, Zhang, Y, Wang, X, and Chen, Y. Biosensor Integrated Tissue Chips and Their Applications on Earth and in Space. Biosens Bioelectron (2023) 222:114820. doi:10.1016/j.bios.2022.114820

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Tran, QD, Tran, NN, and Hessel, V. Frontier Medical Technologies to Support Space Exploration. In Space Manufacturing and Resources (John Wiley and Sons, Ltd) (2022). 47–65. doi:10.1002/9783527830909.ch3

CrossRef Full Text | Google Scholar

9. Krüger, M, Pietsch, J, Bauer, J, Kopp, S, Carvalho, DTO, Baatout, S, et al. Growth of Endothelial Cells in Space and in Simulated Microgravity – A Comparison on the Secretory Level. Cell. Physiol. Biochem. (2019) 52:1039–60. doi:10.33594/000000071

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Pietsch, J, Gass, S, Nebuloni, S, Echegoyen, D, Riwaldt, S, Baake, C, et al. Three-Dimensional Growth of Human Endothelial Cells in an Automated Cell Culture Experiment Container during the SpaceX CRS-8 ISS Space Mission – The SPHEROIDS Project. Biomaterials (2017) 124:126–56. doi:10.1016/j.biomaterials.2017.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Liu, X, Ma, D, Ye, H, Hou, Y, Bai, X, Xing, Y, et al. Electrowetting-based Digital Microfluidics: Toward a Full-Functional Miniaturized Platform for Biochemical and Biological Applications. Trac, Trends Anal Chem (2023) 166:117153. doi:10.1016/j.trac.2023.117153

CrossRef Full Text | Google Scholar

12. Min, X, and Kim, WS. Beyond High Voltage in the Digital Microfluidic Devices for an Integrated Portable Sensing System. Microfluid Nanofluid (2019) 23:127–14. doi:10.1007/s10404-019-2294-y

CrossRef Full Text | Google Scholar

13. Wikramanayake, E, Hale, R, Elam, J, Shahriari, A, Bahadur, V, Alvarez-Hernandez, AR, et al. “Characterizing Microfluidic Operations Underlying an Electrowetting Heat Pipe on the International Space Station,” in Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, November 9–15, 2018. Vol. 7 (ASME) (2019). doi:10.1115/IMECE2018-86223

CrossRef Full Text | Google Scholar

14. Nijhuis, J, Schmidt, S, Tran, NN, and Hessel, V. Microfluidics and Macrofluidics in Space: ISS-Proven Fluidic Transport and Handling Concepts. Front Space Technol (2022) 2:779696. doi:10.3389/frspt.2021.779696

CrossRef Full Text | Google Scholar

15. Wang, M, Fu, Q, Liu, R, Wang, C, Li, X, Sun, X, et al. A Microfluidic Manipulation Platform Based on Droplet Mixing Technology. Chem Eng Sci (2024) 298:120422. doi:10.1016/j.ces.2024.120422

CrossRef Full Text | Google Scholar

16. Paik, P, Pamula, VK, and Fair, RB. Rapid Droplet Mixers for Digital Microfluidic Systems. Lab Chip (2003) 3:253–9. doi:10.1039/B307628H

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Samiei, E, Tabrizian, M, and Hoorfar, M. A Review of Digital Microfluidics as Portable Platforms for Lab-On A-Chip Applications. Lab Chip (2016) 16:2376–96. doi:10.1039/C6LC00387G

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lu, Y, Zhang, M, Zhang, H, Huang, J, Wang, Z, Yun, Z, et al. On-chip Acoustic Mixer Integration of Electro-Microfluidics towards In-Situ and Efficient Mixing in Droplets. Microfluid Nanofluid (2018) 22:146–12. doi:10.1007/s10404-018-2169-7

CrossRef Full Text | Google Scholar

19. Mugele, F, Baret, J-C, and Steinhauser, D. Microfluidic Mixing through Electrowetting-Induced Droplet Oscillations. Appl Phys Lett (2006) 88:204106. doi:10.1063/1.2204831

CrossRef Full Text | Google Scholar

20. Zhang, T, Zhou, P, Simon, T, and Cui, T. Internal Flow in Sessile Droplets Induced by Substrate Oscillation: Towards Enhanced Mixing and Mass Transfer in Microfluidic Systems. Microsyst Nanoeng (2024) 10:86–11. doi:10.1038/s41378-024-00714-4

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Bono, S, Kinugasa, H, Kajita, H, and Konishi, S. Resonant Oscillation of Droplets Under an Alternating Electric Field to Enhance Solute Diffusion. Sci Rep (2024) 14:21326–8. doi:10.1038/s41598-024-72089-5

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Miraghaie, R, Sterling, JD, and Nadim, A. Shape Oscillation and Internal Mixing in Sessile Liquid Drops Using Electrowetting-On-Dielectric (EWOD). ResearchGate (2006) 2:610–3.

Google Scholar

23. Lee, JH, Lee, KH, Won, JM, Rhee, K, and Chung, SK. Mobile Oscillating Bubble Actuated by AC-Electrowetting-On-Dielectric (EWOD) for Microfluidic Mixing Enhancement. Sens Actuators, A (2012) 182:153–62. doi:10.1016/j.sna.2012.05.022

CrossRef Full Text | Google Scholar

24. Bansal, S, and Sen, P. Mixing Enhancement by Degenerate Modes in Electrically Actuated Sessile Droplets. Sens Actuators, B (2016) 232:318–26. doi:10.1016/j.snb.2016.03.109

CrossRef Full Text | Google Scholar

25. Hu, Q, Ren, Y, Liu, W, Chen, X, Tao, Y, and Jiang, H. Fluid Flow and Mixing Induced by AC Continuous Electrowetting of Liquid Metal Droplet. Micromachines (2017) 8:119. doi:10.3390/mi8040119

CrossRef Full Text | Google Scholar

26. Lee, C-P, Chen, H-C, and Lai, M-F. Electrowetting on Dielectric Driven Droplet Resonance and Mixing Enhancement in Parallel-Plate Configuration. Biomicrofluidics (2012) 6:12814–128148. doi:10.1063/1.3673258

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Wei, Y, Zou, J, Zhou, C, Li, F, and Zhao, Z. Numerical Investigation of Micro-Droplets Mixing in Electrowetting-On-Dielectric Digital Microfluidics: The Merging Process and Frequency Response. Phys Fluids (2022) 34:102009. doi:10.1063/5.0114475

CrossRef Full Text | Google Scholar

28. Malk, R, Fouillet, Y, and Davoust, L. Rotating Flow within a Droplet Actuated with AC EWOD. Proced Chem (2009) 1:1107–10. doi:10.1016/j.proche.2009.07.276

CrossRef Full Text | Google Scholar

29. Hong, FJ, Jiang, DD, and Cheng, P. Frequency-dependent Resonance and Asymmetric Droplet Oscillation under Ac Electrowetting on Coplanar Electrodes. J Micromech Microeng (2012) 22:085024. doi:10.1088/0960-1317/22/8/085024

CrossRef Full Text | Google Scholar

30. Berthier, J. Micro-Drops and Digital Microfluidics. Norwich, NY: William Andrew Publishing (2013). doi:10.1016/C2011-0-05581-3

CrossRef Full Text | Google Scholar

31. Yamamoto, Y, Ito, T, Wakimoto, T, and Katoh, K. Numerical and Theoretical Analyses of the Dynamics of Droplets Driven by Electrowetting on Dielectric in a Hele-Shaw Cell. J Fluid Mech (2018) 839:468–88. doi:10.1017/jfm.2018.16

CrossRef Full Text | Google Scholar

32. Barber, RW, and Emerson, DR. Recent Advances in Electrowetting Microdroplet Technologies. In: Microdroplet Technology. New York, NY, USA: Springer (2012). p. 77–116. doi:10.1007/978-1-4614-3265-4_4

CrossRef Full Text | Google Scholar

33. Guan, Y, Li, B, and Xing, L. Numerical Investigation of Electrowetting-Based Droplet Splitting in Closed Digital Microfluidic System: Dynamics, Mode, and Satellite Droplet. Phys Fluids (2018) 30:112001. doi:10.1063/1.5049511

CrossRef Full Text | Google Scholar

34. Bouillant, A, Cohen, C, Clanet, C, and Quéré, D. Self-excitation of Leidenfrost Drops and Consequences on Their Stability. Proc Natl Acad Sci USA (2021) 118:e2021691118. doi:10.1073/pnas.2021691118

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Dong, J, Liu, Y, Xu, Q, Wang, Y, and Wang, S. Surface Parametric Instability of Star-Shaped Oscillating Liquid Drops. Phys Fluids (2019) 31:087104. doi:10.1063/1.5112007

CrossRef Full Text | Google Scholar

36. Brunet, P, and Snoeijer, JH. Star-Drops Formed by Periodic Excitation and on an Air Cushion - a Short Review. The Eur Phys J Spec Top (2011) 192:207–26. doi:10.1140/epjst/e2011-01375-5

CrossRef Full Text | Google Scholar

37. Okada, M, and Okada, M. Observation of the Shape of a Water Drop on an Oscillating Teflon Plate. Experiments in Fluids (2006) 41:789–802. doi:10.1007/s00348-006-0203-0

CrossRef Full Text | Google Scholar

38. Pang, X, Duan, M, Liu, H, Xi, Y, Shi, H, and Li, X. Oscillation-induced Mixing Advances the Functionality of Liquid Marble Microreactors. ACS Appl Mater and Inter (2022) 14:11999–2009. doi:10.1021/acsami.1c22314

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Chang, C-T, Bostwick, JB, Daniel, S, and Steen, PH. Dynamics of Sessile Drops. Part 2. Experiment. J Fluid Mech (2015) 768:442–67. doi:10.1017/jfm.2015.99

CrossRef Full Text | Google Scholar

40. Mampallil, D, Burak Eral, H, Staicu, A, Mugele, F, and van den Ende, D. Electrowetting-driven Oscillating Drops Sandwiched between Two Substrates. Phys Rev E (2013) 88:053015. doi:10.1103/PhysRevE.88.053015

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Shen, CL, Xie, W, Yan, ZL, and Wei, B. Internal Flow of Acoustically Levitated Drops Undergoing Sectorial Oscillations. Phys Lett A (2010) 374:4045–8. doi:10.1016/j.physleta.2010.07.071

CrossRef Full Text | Google Scholar

42. Theisen, J, and Davoust, L. Mass Transfer Enhancement and Surface Functionalization in Digital Microfluidics Using AC Electrowetting: The Smaller, the Better. Microfluid Nanofluid (2015) 18:1373–89. doi:10.1007/s10404-014-1536-2

CrossRef Full Text | Google Scholar