Abstract
High-speed aircraft experiences severe aerodynamic heating at high Mach numbers, requiring accurate prediction of aerothermal heating effects before designing thermal protection systems. With the rise of artificial intelligence and the potential of neural networks, data-driven methods for aerothermal heating prediction have gained significant attention. This study focuses on numerical simulations of aerothermal heating phenomena and explores machine learning applications in heat prediction. First, a two-dimensional cylinder case was simulated using the finite volume method with chemical non-equilibrium flow to understand flow characteristics and heat distribution. Subsequently, Two aerothermal heating datasets were established: the first varies Mach number from 7.0 to 11.9 under fixed freestream conditions, while the second combines Mach numbers (8.5–9.5) with varying temperatures (890 K, 901 K, 910 K) and pressures (460 Pa, 470 Pa, 476 Pa). And the influence of incoming flow conditions on shock waves, temperature fields, wall heat flux was analyzed. Finally, machine learning methods were applied to predict aerothermal heating properties. A multilayer perceptron (MLP) prediction model was established to predict wall heat flux, the reverse line from the stagnation point along the flow direction pressure and temperature, as well as the temperature and pressure fields. Additionally, a convolutional neural network (CNN) model was developed to accurately predict the temperature and pressure fields. While the MLP model demonstrates strong predictive accuracy for physical quantities along the cylinder surface and the reverse line from the stagnation point along the flow direction, the CNN model exhibits superior performance in predicting the entire flow field. Compared to the numerical simulation methods used, the established model can quickly predict the aerothermal environment of a two-dimensional cylinder, helping to shorten the design cycle of thermal protection systems.
Introduction
When an aircraft flies at high speeds, the friction between the surface of the fuselage and the airflow causes intense heat generation. The air is subjected to stagnation and compression, leading to a rapid increase in temperature. The high-temperature gas transfers heat to the lower-temperature aircraft surface, resulting in aerothermal heating. Aerothermal heating can compromise the structural stability. However, factors such as viscous interference, high-temperature gas effects, scale effects, and shock wave-boundary layer interactions in high-speed flows significantly increase the difficulty of predicting aerothermal heating [1].
Current aerothermal environment prediction methods can generally be classified into three categories: experimental methods, engineering calculation methods, and numerical methods [2–4].
Aerothermal experimental methods can generally be divided into ground-based and flight testing methods. Ground-based tests primarily use wind tunnels, where aerothermal data measurement can be achieved through contact-based point measurement methods and non-contact measurement methods. In contrast, flight test data can only be obtained through contact-based point measurement methods [5]. Contact-based point measurement uses sensors, offering high precision but limited data. Non-contact measurement is typically performed using optical methods to directly obtain the aerothermal distribution, though the accuracy is generally lower.
Aerothermal engineering algorithms are primarily derived through the boundary layer equation self-similarity theory, or by analyzing and fitting experimental data to obtain semi-empirical formulas [6]. For example, for axisymmetric objects, the Kemp-Riddell formula [7] and the Fay-Riddell formula [8] can be used to solve for stagnation point aerothermal heating. The Lees formula [9] and the modified Lees formula [10] are used to calculate the laminar flow regions excluding the stagnation point. The turbulent viscous-inviscid interaction (TVI) model [11] can be applied to calculate the turbulent regions excluding the stagnation point.
Compared to aerothermal testing and engineering algorithms, aerothermal numerical simulation, specifically Computational Fluid Dynamics (CFD), is currently more widely applied. Compared to wind tunnel testing, CFD can simulate the entire flight envelope of an aircraft [12]. Compared to engineering estimation methods, CFD offers higher precision. Furthermore, CFD eliminates the need to scale the aircraft size, which is crucial for predicting the aerothermal loads on the aircraft [13]. Although numerical methods can be applied to most problems, the results are influenced by numerous factors. When using CFD for aerothermal calculations, even with the same governing equations, different numerical schemes can lead to varying results. Some numerical schemes may even produce incorrect results, such as the “Carbuncle” phenomenon [14]. Chen [15] pointed out that common numerical schemes cannot completely avoid this phenomenon. Different wall catalytic conditions have a significant impact on heat flux calculations [16]. However, due to the complexity of the catalytic reaction mechanism and the difficulty of measurement in experiments, most calculations simplify these conditions, which sometimes leads to considerable errors. Scott [17] compared non-equilibrium computational methods with spacecraft flight test data and found that neglecting the catalytic conditions on the wall led to excessive thermal protection design. In addition, aerothermal prediction problems typically require large grid quantities [18], and the slow convergence of calculations, such as wall heat flux [19], significantly increases the computational time.
In recent years, with the rise of artificial intelligence and the demonstrated potential of neural networks across various fields, data-driven flow field modeling and numerical simulations have gained increasing attention and achieved significant progress [20]. Liu et al. [6] employed 60 sets of 2D cylindrical computational samples under different inflow conditions with fluid-thermal-structural coupling, and developed a rapid prediction model for multiphysics fields using Proper Orthogonal Decomposition (POD) combined with Radial Basis Function (RBF) algorithms. Ding et al. [21] developed an Artificial Neural Network (ANN)-based aerothermal heating prediction model with 57 sets of Direct Simulation Monte Carlo (DSMC) simulation data. Ren et al. [22] established a physics-informed Deep Neural Network (DNN) framework for aerothermal heating prediction with only 6 RANS solutions and flight data. Among the numerous machine learning methods, Multilayer Perceptron (MLP) [23], a key technology in machine learning, is capable of handling complex nonlinear relationships and exhibits strong generalization ability, drawing significant attention from researchers. Convolutional Neural Networks (CNN) [24], a major technology in deep learning, are especially effective at capturing local features and efficiently processing high-dimensional multidimensional data, particularly when there is temporal or spatial correlation in the data. In the aerospace field, scholars have used MLP model to predict aerodynamic characteristics of wings [25] and temperature fields [26], and CNN model to predict flow fields [27], aerothermal heating [28], and wall heat flux [29], achieving promising prediction results.
For aerothermal environment prediction, the flow around a cylinder is one of the most fundamental problems. Novello et al. [30] established a dataset through the two-dimensional cylinder flow problem and used deep learning methods to accelerate aerothermal numerical simulations. However, their work primarily focuses on accelerating the numerical simulation of chemical reactions. Gkimisis et al. [31] used artificial neural networks to predict the flow around a two-dimensional cylinder, but the neural network they employed was too simple, requiring a massive amount of training data. In this work, a multilayer perceptron (MLP) model was established to predict physical quantities both locally (along the cylinder surface and the reverse line from the stagnation point along the flow direction) and globally across the entire flow field, while a convolutional neural network (CNN) model was developed to predict physical quantities across the entire flow field. The freestream Mach number, temperature, and pressure were used as input features, comparing to other methods [31] requiring datasets with thousands of flow fields, our prediction approach achieves promising accuracy using only around one hundred flow fields for aerothermal environment prediction.
In summary, this study aims to predict the aerothermal environment of a two-dimensional cylinder under different freestream Mach numbers, temperatures, and pressures. A finite volume method, considering chemical non-equilibrium flow, was used to numerically simulate the two-dimensional cylinder verification case. Two aerothermal heating datasets were established: the first varies Mach number from 7.0 to 11.9 under fixed freestream conditions, while the second combines Mach numbers (8.5–9.5) with varying temperatures (890 K, 901 K, 910 K) and pressures (460 Pa, 470 Pa, 476 Pa). Two machine learning methods, MLP and CNN, were employed to develop rapid aerodynamic heat prediction models. The predictive capabilities of MLP and CNN models were compared. While the MLP model demonstrates strong predictive accuracy for physical quantities along the cylinder surface and the reverse line from the stagnation point along the flow direction, the CNN model exhibits superior performance in predicting the entire flow field than the MLP modeland the performance of CNN was further evaluated with different input data.
Numerical Simulation Methods and Machine Learning Models
Numerical Simulation Methods
For high-speed flow problems, the variation in air density cannot be ignored, so a multi-species compressible Navier-Stokes equation set [32] should be used, expressed in differential form as shown in Equation 1: is the residual function, representing the remaining part of the equation, which should approach zero to satisfy the equation. is the conservative variables of the flow field, which is shown in Equation 2: represent the densities of different fluid components, is the momentum, is the energy, and is time. is the Nabla operator, representing the gradient of a vector, which is used to describe the spatial rate of change of variables. is the convective fluxs, which includes the momentum and energy of the fluid. is the velocity vector, including the three components of the fluid in the Cartesian coordinate system.
The convective fluxes , viscous fluxes , and source terms are shown in Equation 3 [33]:and is the static pressure, and are, respectively, the total energy per unit mass and the vibrational–electronic energy per unit mass for the mixture, is the total enthalpy per unit mass, is the species mass diffusion flux, is the viscous stress tensor, is the conduction heat flux, index denotes the -th chemical species, and is the total number of species.
The calculation uses the open-source software SU2 [34], the thermodynamic state of the continuous flow is modeled using the rigid rotor harmonic oscillator (RRHO) two-temperature model. Through the independence of energy levels, the total energy per unit volume is shown in Equation 4:Where is the fluid density, is the total energy per unit volume, is the density of the -th species, is the translational energy of the -th species, is the rotational energy of the -th species, is the vibrational energy of the -th species, is the electronic energy of the -th species, and is the fluid velocity vector. The vibrational–electronic energy is shown in Equation 5:
Generally, a gas mixture consists of polyatomic molecules, monatomic species, and free electrons. The expressions for translational, rotational, vibrational, and electronic energies are given below. First, for electrons, , , and are all zero. For monatomic species, and are zero. For all other cases, the expressions for each energy component are shown in Equation 6.
Where is the gas constant, is the gas temperature, is the molar mass of the -th species, is the number of rotational axes (which should be an integer), is the characteristic vibrational temperature of the species, is the characteristic electronic temperature of the corresponding species, and is the degeneracy of the -th state.
Multilayer Perceptron
In this work, a multilayer perceptron (MLP) [35] model is used for prediction. The multilayer perceptron is an artificial neural network structure composed of multiple layers of neurons. Structurally, the MLP consists of an input layer, hidden layers, and an output layer. The input layer receives the input data, with each data point corresponding to one neuron. There can be multiple hidden layers, and each neuron in a hidden layer receives the output from the neurons in the previous layer, then performs a nonlinear transformation through weighted summation and an activation function. The output layer provides the prediction result, with each neuron receiving the output from the final hidden layer and applying an activation function to it. The number of neurons in the output layer corresponds to the number of output values or categories in the prediction result.
In the hidden layers and output layer, each neuron typically applies an activation function to introduce non-linearity. In this work, the activation function used is the ReLU function [36]. The ReLU function maps negative values to 0 and keeps positive values unchanged. ReLU function is one of the most commonly used activation functions and is sufficient for the vast majority of machine learning models. Its mathematical form is shown in Equation 7When training the multilayer perceptron model, it is necessary to define a loss function to measure the difference between the model’s predictions and the true labels. In this work, the loss function used is the Mean Squared Error (MSE). MSE is used to calculate the average of the squared differences between the predicted values and the true values. Its mathematical expression is shown in Equation 8where is the true label, is the model’s predicted value, and is the number of samples.
Convolutional Neural Networks
Convolutional Neural Networks (CNN) [37] can combine multiple convolutional layer and sampling layers to process input signals and achieve mapping to output targets in the fully connected layers. In a CNN, each feature map is a plane composed of multiple neurons, and input features are extracted using convolutional filters. Each convolutional layer contains multiple feature maps. The sampling layers perform subsampling based on the principle of local correlation, thereby reducing the amount of data while preserving valuable information.
The composite process of the convolutional and sampling layers in a CNN can be summarized as follows: For example, the first convolutional layer after the input layer has 8 feature maps, each of which is a array of neurons. Each neuron extracts local features from the input layer using convolutional filters. In the sampling layer, each neuron is connected to a neighborhood in the corresponding feature map of the previous layer. As a result, the sampling layer has 8 feature maps, each sized The next convolutional layer then applies convolution to the sampling layer, and the subsequent sampling layer continues to subsample the previous convolutional layer. Ultimately, the input is mapped to a multidimensional feature vector, which is then processed by the fully connected layer and the output layer to complete the recognition task.
In this work, the activation function used in the convolutional neural network is the ReLU function, and the loss function used is the Mean Squared Error (MSE).
The MLP excels at handling nonlinear relationships and is well-suited for predicting physical quantities on curves and reconstructing entire flow fields. In contrast, CNN efficiently process multidimensional information and appear more effective for reconstructing complete flow fields. While some researchers have compared these two approaches [38, 39] in domains like image processing, this study adopts both MLP and CNN methods to predict aerothermal heating and conducts a comparative analysis of their performance in flow field prediction.
Numerical Simulation of the Aerothermal Heating
Convergence and Grid Independence Verification of the Solution
In grid studies related to aerothermal heating, most researchers focus on the grid Reynolds number [40], which is shown in Equation 9That is, the grid Reynolds number is defined using as the characteristic length scale, where is typically taken as the height of the first layer of the grid in the boundary layer. The grid Reynolds number is used to reflect the density of the grid near the wall. For heat flux calculations, the finer the grid near the wall, the closer the calculated results are to the true values.
In this work, a two-dimensional cylinder with a radius of is selected as a case study, and experimental data from the Göttingen (HEG) high-enthalpy shock tunnel [41] is used to validate the accuracy of the numerical algorithm. The thermochemical nonequilibrium relaxation process occurring within the shock layer, which affects the density distribution of air components, is typically used to validate the physical and chemical models implemented in CFD codes. The two-dimensional cylinder is chosen as a common computational example for hypersonic flows due to the availability of extensive related data, which facilitates the validation of computational results. Additionally, the relatively low complexity of the two-dimensional cylinder flow field makes the computation more convenient, aiding in the subsequent establishment of datasets.
The mesh consists of 29,651 cells, and the Reynolds number is 10,643. The air model used is a five-species gas model with chemically non-equilibrium flow, neglecting high-temperature ionization effects and wall catalysis effects. The wall temperature is set to 300 K, and the numerical scheme employed is the AUSM+ format. The computational mesh is shown in the Figure 2, and the computational conditions are listed in Table 1.
TABLE 1
| 5956 | 476 | 1.57e-3 | 901 | 8.98 | 0.75431 | 0.00713 | 0.01026 | 6.5e-7 | 0.22831 |
HEG test free flow conditions and air composition.
The convergence of pressure and heat flux with respect to the number of iterations and grid density is shown in Figure 1. According to the graph, the pressure initially increases gradually and then stabilizes, reaching near stability around 500,000 iterations, with a relatively fast convergence rate. The heat flux starts with a large value, then decreases rapidly. After about 400,000 iterations, the rate of decrease slows down, and it essentially converges around 750,000 iterations.
FIGURE 1
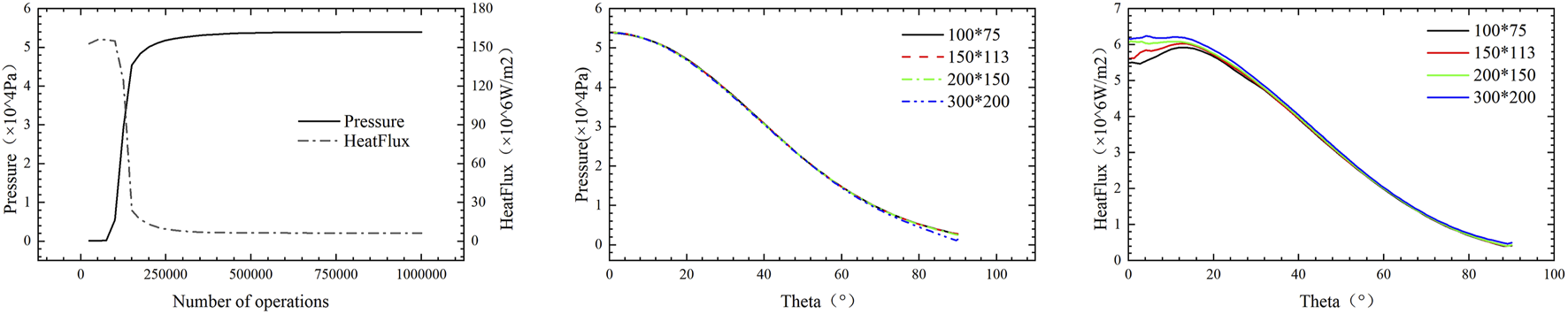
Convergence of pressure and heat flux with respect to the number of iterations and grid density.
The reference length of the two-dimensional cylinder in this work is . Regarding the effect of grid density on the pressure calculation results, starting with a grid (Grid I),with a first-layer grid height of , the number of grid nodes was increased to (Grid II), with a first-layer grid height of , (Grid III), with a first-layer grid height of , and (Grid IV), with a first-layer grid height of .with corresponding grid Reynolds numbers. From the graph, it can be observed that for the heat flux calculation, the grid density should be greater than , and the corresponding grid Reynolds number should be less than 0.02365, for the pressure calculation, the computational results for these four grid types show good agreement and are all acceptable, the differences at theta of 90°, the discrepancy observed at arises from subtle influences of the outlet boundary conditions on the simulation results.
In conclusion, when the grid has nodes, the grid Reynolds number is smaller than 0.02365, and the number of iterations exceeds 750,000 steps, the calculation results can be considered converged.
Case Study Validation
The computational results are compared with experimental and numerical results from other researchers [42], as shown in Figure 2. For the pressure calculations, the results align well with both experimental data and simulation data from the literature [42]. For the heat flux calculations, the predicted values are slightly lower than the experimental data, particularly in the stagnation region. This under-prediction is due to the lack of catalytic effects. Knight et al. [41] suggest that accurate prediction of surface heat flux requires consideration of catalytic effects. Compared to other non-catalytic results from Nompelis [43] and Maier [42], Nompelis employed a modified Steger–Warming flux splitting scheme, while Maier employed the AUSM+ format, the results in this work lie between the two and show a better match with experimental data, especially near the stagnation point. This confirms the correctness of the numerical simulation method used in this work.
FIGURE 2
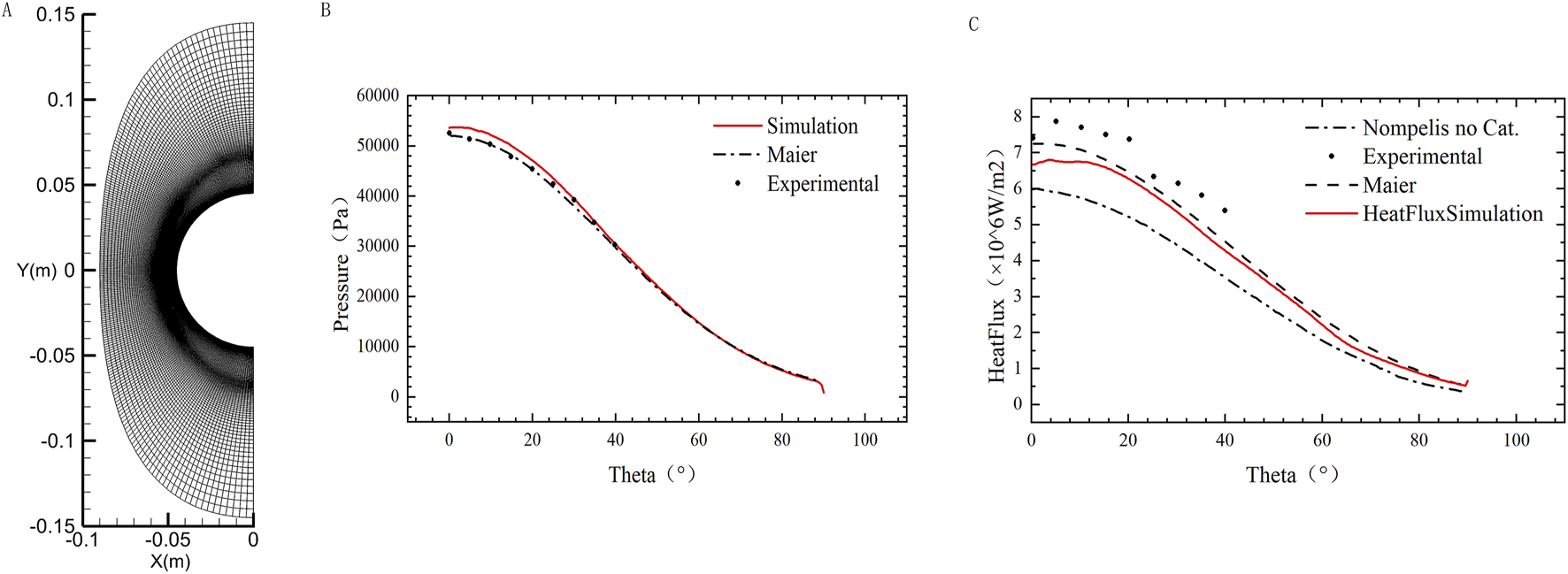
Computational grid (A) and comparison of pressure (B) and heatflux calculation (C) results with papers and experiments.
Machine Learning Prediction Results and Discussion
Establishment of the Aerodynamic Heating Datasets
For the aerodynamic heating prediction problem, during numerical calculations, as shown in Table 1, the temperature, pressure, velocity, density, and gas composition of the free-stream flow are the key factors affecting the calculation results. For the standard atmosphere, the temperature, pressure, density, and air composition are closely related to altitude, while the variation in density and air composition is minimal within small altitude ranges. In this work, the aerodynamic heating datasets were first established by varying the Mach number as a single variable, followed by changes in the incoming flow temperature and pressure, combined with the Mach number. Three variables are used to construct the aerodynamic heating datasets. Two aerothermal heating datasets were constructed in total. Apart from the changing variables, other parameters used for constructing the datasets are consistent with those in Tables 1. The mesh used consists of 150 nodes in the streamwise direction and 200 nodes along the wall direction, with the first layer of the boundary layer set to a height of . The dataset for the single Mach number variation spans from Mach 7.0 to Mach 11.9, with a step size of 0.1, resulting in a total of 50 computation results. The dataset constructed using three variables includes Mach numbers ranging from 8.5 to 9.5, with pressures of 460 Pa, 470 Pa, and 476 Pa, and temperatures of 890 K, 901 K, and 910 K, resulting in a total of 99 computation results.
Neural Network Model Parameter Settings
Based on the datasets generated above, the study first uses MLP model to investigate single-parameter input and multi-parameter inputs. Then, MLP and CNN models were used for full-field prediction with single-parameter input. During the solving process, the pressure calculation converges more easily and is less affected by various factors. The network structure of the MLP models are shown in Tables 2, 3 and Figure 3. In Tables 2, 3, the 200 neurons in the output layer represent 200 discrete nodes distributed along the cylindrical wall surface. In Figure 3, the 30,000 neurons in the output layer correspond to 30,000 nodes spanning the entire computational flow field.
TABLE 2
| Serial No. | Network Type | Activation Function | Number of Neurons |
|---|---|---|---|
| 1 | Input Layer | ReLU | 1 |
| 2 | Hidden Layer | ReLU | 16 |
| 3 | Hidden Layer | ReLU | 64 |
| 4 | Hidden Layer | ReLU | 128 |
| 5 | Output Layer | - | 200 |
MLP network structure with free-stream Mach number as input.
TABLE 3
| Serial No. | Network Type | Activation Function | Number of Neurons |
|---|---|---|---|
| 1 | Input Layer | ReLU | 3 |
| 2 | Hidden Layer | ReLU | 16 |
| 3 | Hidden Layer | ReLU | 64 |
| 4 | Hidden Layer | ReLU | 128 |
| 5 | Output Layer | - | 200 |
MLP network structure with free-stream Mach number, pressure and temperature as inputs.
FIGURE 3
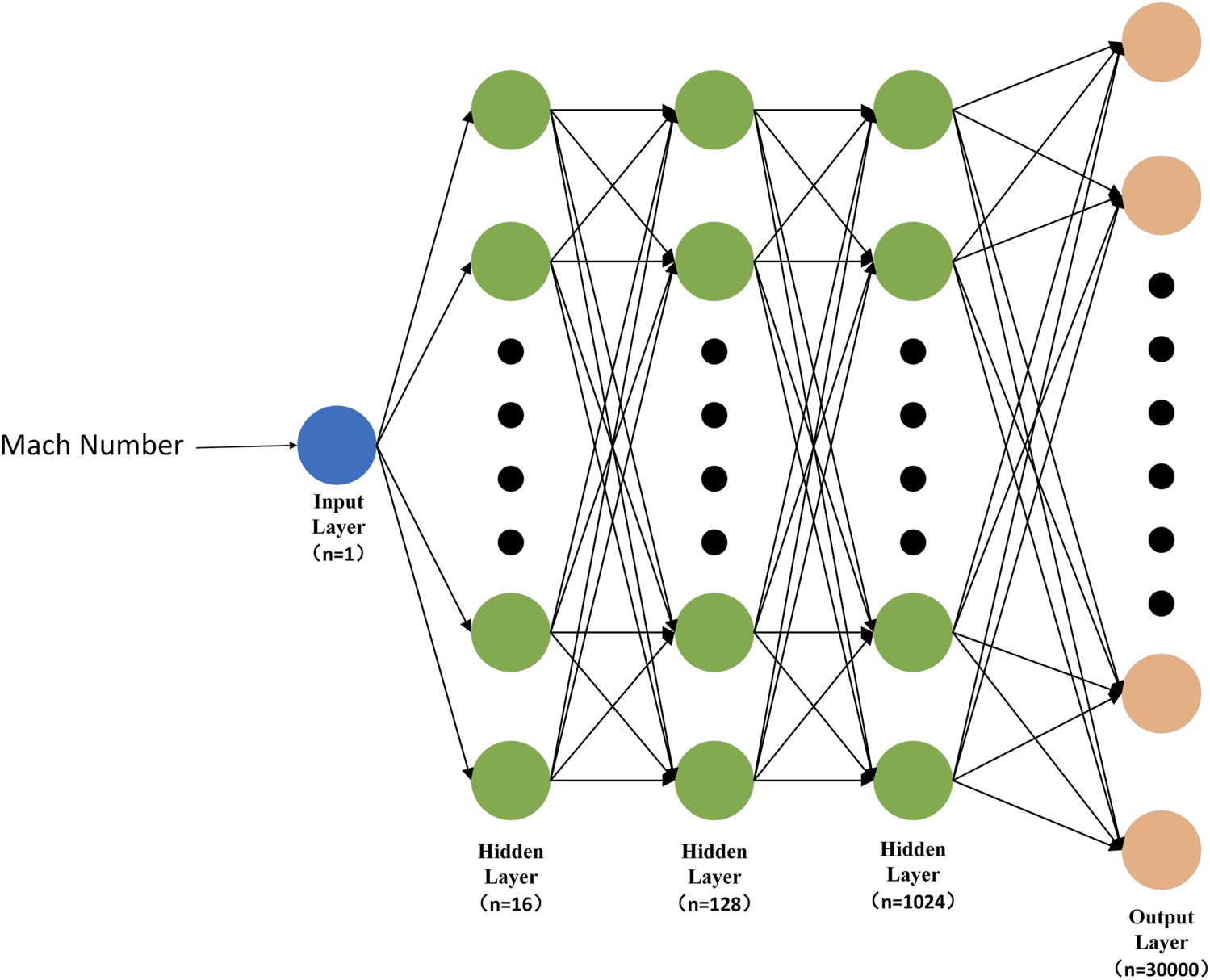
Schematic diagram of the Multilayer Perceptron (MLP) model with prediction of the entire flow field.
The schematic diagram of the CNN model is shown in Figure 4 and the network structure for CNN model predicting the full-field parameters is shown in Table 4. Pooling layers enhance computational efficiency and feature robustness through dimensionality reduction (their absence causes computational redundancy and sensitivity to minor input variations), while unpooling layers restore lost spatial details (missing them leads to blurry reconstructions or localization inaccuracies). The inputs consist of three channels, which represent the incoming Mach number and the x and y coordinates of the grid nodes. The output consists of two channels: pressure and temperature.
FIGURE 4
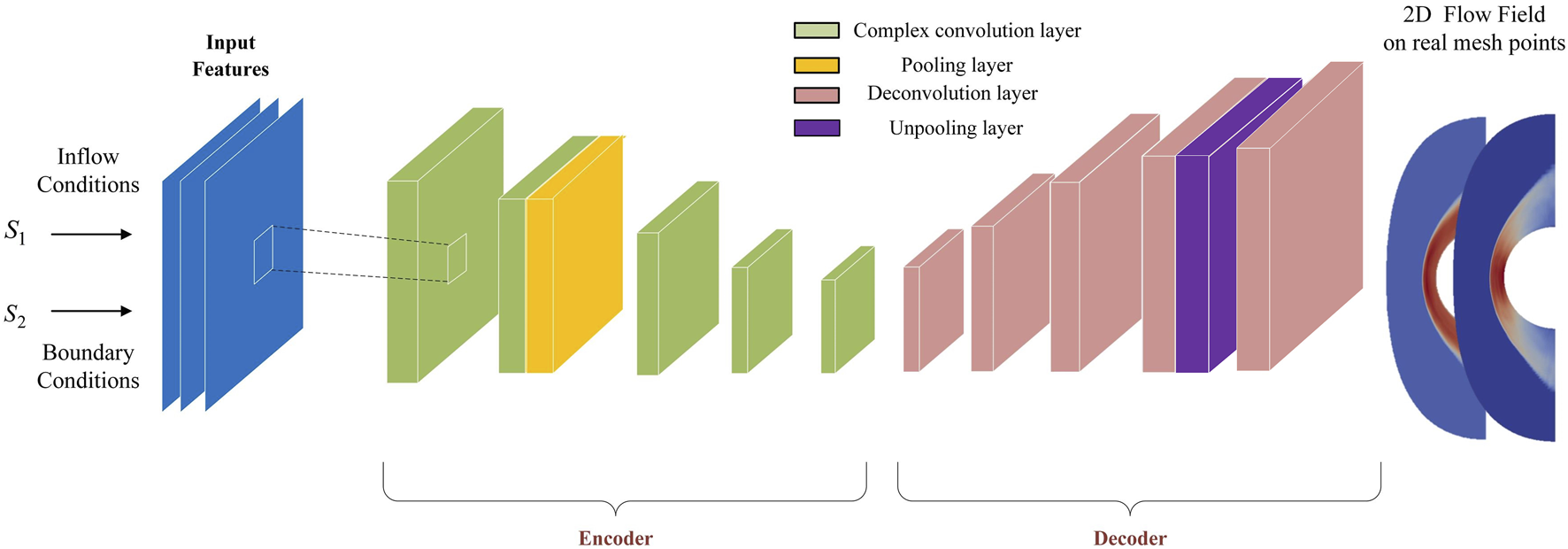
Schematic diagram of the Convolutional Neural Network (CNN) model.
TABLE 4
| Serial No. | Network Type | Activation Function | Number of Neurons |
|---|---|---|---|
| 1 | Input Layer | - | 3 |
| 2 | Convolution | ReLU | 8 |
| 3 | Convolution + Pooling | ReLU | 16 |
| 4 | Convolution | ReLU | 32 |
| 5 | Convolution | ReLU | 64 |
| 6 | Convolution | ReLU | 128 |
| 7 | Deconvolution | ReLU | 128 |
| 8 | Deconvolution | ReLU | 64 |
| 9 | Deconvolution | ReLU | 32 |
| 10 | Deconvolution + Unpooling | ReLU | 16 |
| 11 | Deconvolution | ReLU | 8 |
| 12 | Output Layer | - | 2 |
CNN network structure with free-stream Mach number and the x and y coordinates of the grid nodes as inputs.
Prediction Results
Using MLP model with Mach number as input to predict wall heat flux, the comparison between the predicted values and the true values when the Mach number is 7 is shown in Figure 5. The wall heat flux is predicted using Mach number, temperature, and pressure as inputs. When the Mach number is 8.5, the temperature is 901K, and the pressure is 476Pa, the comparison between the predicted value and the true value is shown in Figure 6. The “HeatFlux” is the wall heat flux, the X represents the distance from a point on the axis of symmetry of the semicircle to the center (with the direction opposite to the flow direction considered positive), and the raw data represents the simulation results. Due to the sharp discontinuity in shock position and the degraded predictive accuracy near the shock wave, significant oscillations are generated at the shock location. Using MLP with the Mach number as input to predict the temperature and pressure of the full field, the comparison between the predicted values and the true values when the Mach number is 7 is shown in Figure 7. Using CNN with the Mach number as input to predict the temperature and pressure of the full field, the comparison between the predicted values and the true values when the Mach number is 7 is shown in Figure 8. In Figures 7, 8, from left to right, the first column is the true values, the second column is the predicted values, and the third column is the relative difference between the predicted and true valuessimulation results. The relative difference is shown in Equation 10
FIGURE 5
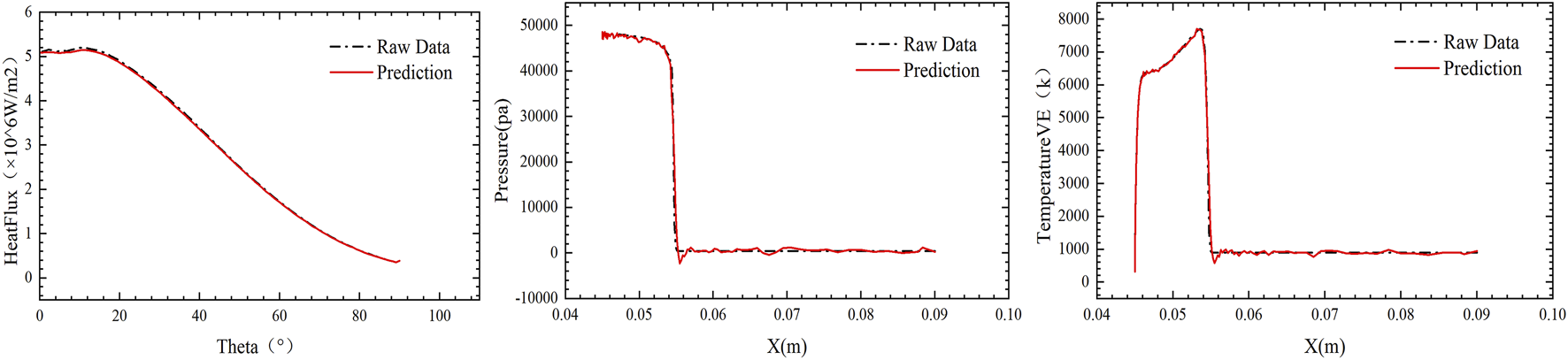
Prediction results of heat flux, pressure, and temperature based on MLP when freestream Mach number is 7.
FIGURE 6
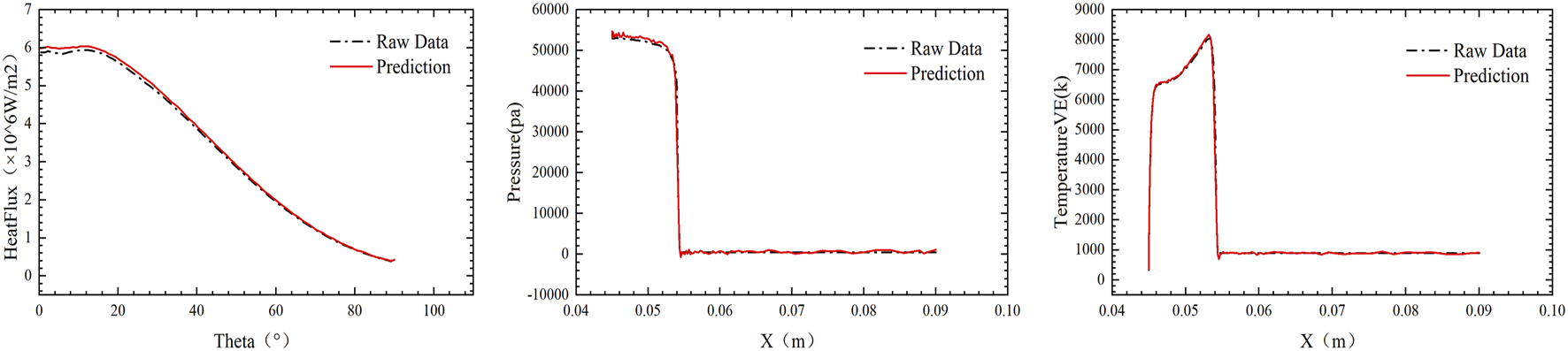
Prediction results of heat flux, pressure, and temperature based on MLP when freestream Mach number is 8.5, pressure is 476 pa, temperature is 901 k.
FIGURE 7
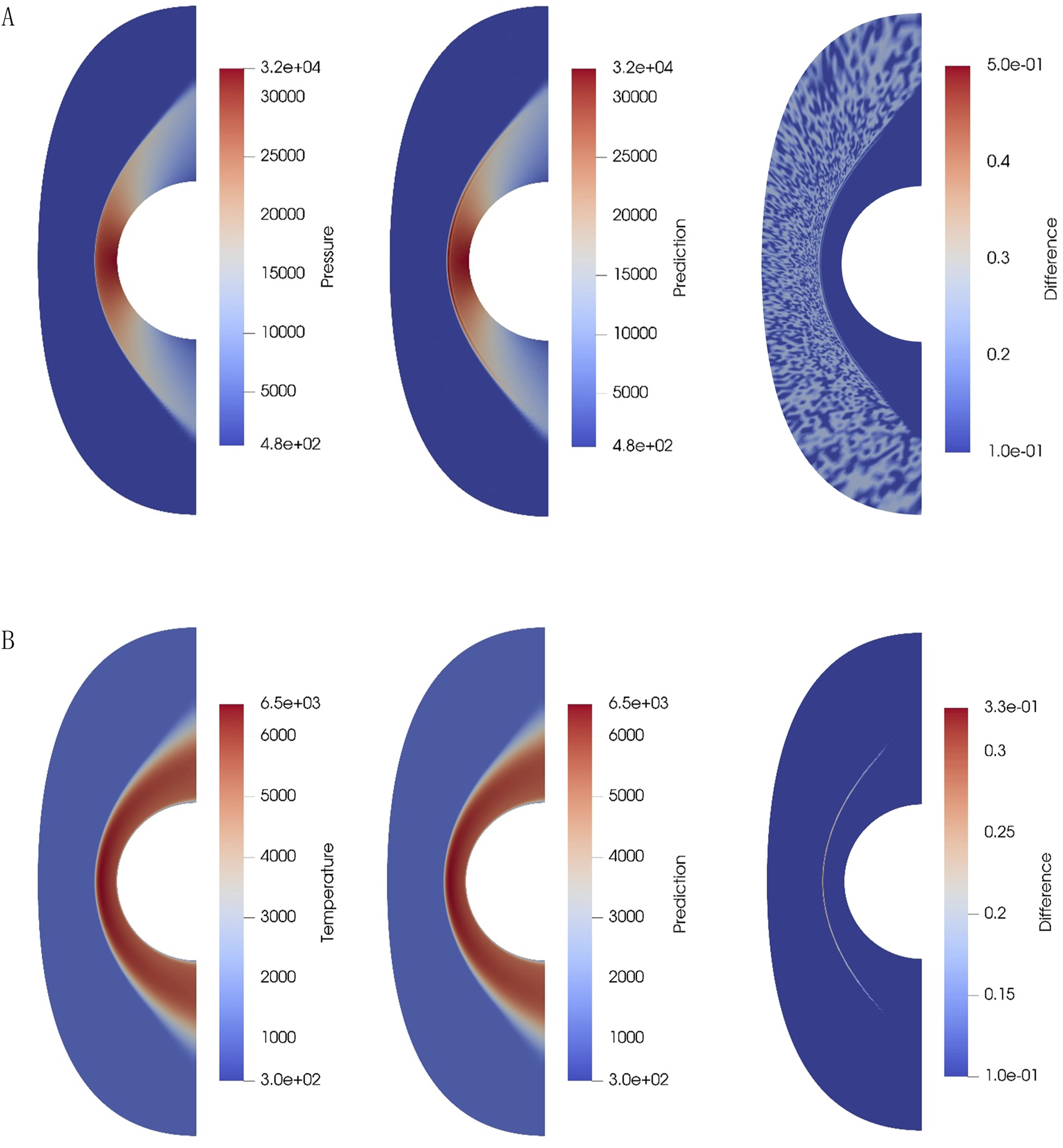
Prediction results of pressure (A) and temperature (B) for the entire flow field based on MLP, when freestream Mach number is 7.
FIGURE 8
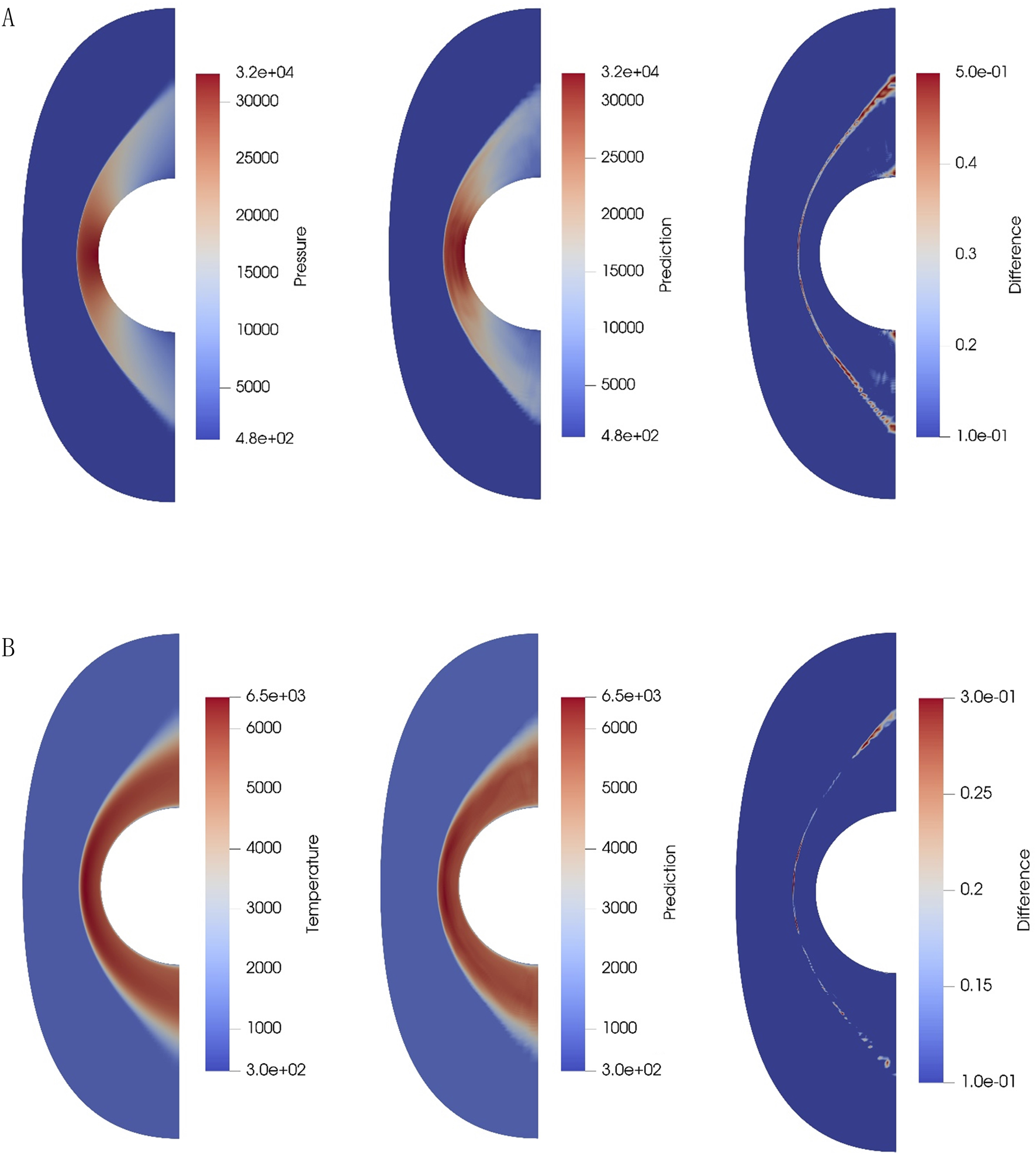
Prediction results of pressure (A) and temperature (B) for the entire flow field based on CNN, when freestream Mach number is 7.
Using MLP model with Mach number as input, wall heat flux, the reverse line from the stagnation point along the flow direction temperature, and pressure are predicted, with an average relative error of 0.89%. Next, MLP mdoel is used with incoming Mach number, temperature, and pressure as inputs to predict wall heat flux, the reverse line from the stagnation point along the flow direction temperature, and pressure, achieving an average relative error of 0.73%. MLP model performs well in predicting physical quantities along the curve. Then, MLP model is used with Mach number as input to predict the temperature and pressure in the entire flow field. Computing aerothermal heating data for a single flow condition (e.g., freestream Mach 7, temperature 901 K, pressure 476 Pa) requires approximately 437.5 core-hours using CFD methods. In contrast, training the MLP model for full-field temperature/pressure prediction takes 2.22 h (2 s 4000 epochs), while the CNN model requires a comparable 2.22 h (4 s 2000 epochs). Once trained, both MLP and CNN models achieve rapid prediction of a single flow condition in a mere 0.15 s. The average relative error for pressure prediction is 7.6%, and for temperature prediction, it is 1.5%. Using CNN model with Mach number and flow field node coordinates as input, the average relative error for pressure prediction is 4.43%, and for temperature prediction, it is 3.34%. The comparisons of prediction errors between CNN and MLP models for temperature and pressure field predictions within the Mach number range of 7.7–8.6 are shown in Table 5. Both MLP and CNN models exhibit less accurate predictions for pressure fields compared to temperature fields across the entire flow domain. As shown in Figures 5, 6, the pressure undergoes abrupt changes (nearly two orders of magnitude difference) across the shock front, whereas the temperature gradually decreases post-shock, eventually aligning with the wall temperature at the boundary with less than one order of magnitude variation. This disparity in gradient magnitudes (Pressure exhibits an order-of-magnitude steeper gradient than temperature) leads to significantly poorer predictive performance for pressure in both models. For temperature field prediction, the CNN model exhibits nearly twice the error of the MLP model. Conversely, the MLP model demonstrates approximately double the error of the CNN model for pressure field predictions. As previously discussed, the challenge in pressure prediction stems from sharp gradients at shock positions, where the CNN’s localized feature extraction capability outperforms the MLP’s global approximation. Critically, total error of the CNN model is lower than that of the MLP, highlighting its balanced performance in multiphysics flow modeling. Overall, CNN model outperforms MLP model in predicting the flow field, and CNN model achieves higher accuracy in the post-shock and wall-adjacent regions. The error mainly occurs at the shock location.
TABLE 5
| Mach Number | Difference of T | Difference of P | ||
|---|---|---|---|---|
| CNN | MLP | CNN | MLP | |
| 7.7 | 3.27% | 1.77% | 3.69% | 9.46% |
| 7.8 | 3.40% | 1.93% | 4.15% | 8.57% |
| 7.9 | 3.36% | 2.08% | 4.07% | 9.47% |
| 8.0 | 3.30% | 1.81% | 4.10% | 10.45% |
| 8.1 | 3.32% | 1.60% | 4.17% | 10.73% |
| 8.2 | 3.90% | 2.13% | 5.15% | 10.78% |
| 8.3 | 3.32% | 1.72% | 4.34% | 8.71% |
| 8.4 | 3.33% | 2.22% | 4.43% | 10.60% |
| 8.5 | 3.36% | 1.75% | 4.55% | 9.28% |
| 8.6 | 4.02% | 1.59% | 5.52% | 10.42% |
Comparisons of prediction errors between CNN and MLP models for temperature and pressure field predictions within the Mach number range of 7.7–8.6.
Conclusion
In this work, the objective is to predict the two-dimensional aerodynamic thermal environment of a cylinder under different operating conditions. The impact of varying grid densities on the numerical simulation results is discussed, leading to the establishment of an aerodynamic thermal dataset. The MLP model is used to predict the wall heat flux, while both MLP and CNN models are employed to predict the temperature and pressure in the flow field, with a comparison of their prediction performance. The following conclusions can be drawn:
(1) The results of wall heat flux are significantly influenced by the grid, the flow field temperature is largely influenced by wall conditions, while the flow field pressure is easier to solve accurately.
(2) MLP model performs well in predicting wall heat flux, while CNN model outperforms MLP model in predicting the temperature and pressure of the entire flow field. However, both models show poorer prediction performance for flow field pressure compared to flow field temperature.
(3) The CNN model provides accurate predictions for the temperature and pressure across the entire flow field, achieving the goal of fast and accurate aerodynamic thermal prediction. Moreover, there is further potential for improvement as additional input parameters are incorporated.
Our work applies the proposed method to predict the aerothermal environment of high-speed flow around a cylinder. The next step will be to explore cutting-edge machine learning techniques to perform aerothermal environment predictions more quickly and accurately, while also transferring the prediction methods to more complex problems.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
YuW: Conceptualization (equal); Data curation (lead); Formal analysis (equal); Investigation (lead); Methodology (equal); Writingoriginal draft (lead); Writing–review and editing (equal). YH: Data curation (equal); Investigation (equal); Writing–review and editing (equal). HZ: Data curation (equal); Investigation (equal); Writing–review and editing (equal). YaW: Data curation (equal); Investigation (equal); Methodology (equal). TJ: Funding acquisition (equal); Methodology (equal); editing (equal). FX: Project administration (lead); Data curation (equal); Supervision Conceptualization (equal); Supervision (lead). All authors contributed to the article and approved the submitted version.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors gratefully acknowledge the support of the National Natural Science Foundation of China 527 (Grant No. 92271107).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
References
1.
Anderson JD . Hypersonic and High Temperature Gas Dynamics. Reston, VA: AIAA (2019). 10.2514/4.105142
2.
Luo C Zongmin H Liu Y Jiang Z . Research Progress on Ground-To-Flight Correlation of Aerodynamic Force and Heating Data from Hypersonic Wind Tunnels. J Experiments Fluid Mech (2020) 34(3):78–89.
3.
Zhao J Xie W Yang Q Meng S Yi F Scarpa F . A Dynamic Data-Driven Response Prediction Method for Thermal Protection Tiles and Experimental Validation. Appl Therm Eng (2022) 215:118959. 10.1016/j.applthermaleng.2022.118959
4.
Zhou D Huang D Hao J Wu H Chang C Zhang H . Fault Diagnosis of Gas Turbines with Thermodynamic Analysis Restraining the Interference of Boundary Conditions Based on Stn. Int J Mech Sci (2021) 191:106053. 10.1016/j.ijmecsci.2020.106053
5.
Peng ZY Shi YL Gong HM Li Z Luo Y . Hypersonic Aeroheating Prediction Technique and its Trend of Development. Acta Aeron Astronaut Sin (2015) 36(1):325–45.
6.
Liu J Wang M Li S . The Rapid Data-Driven Prediction Method of Coupled Fluid–Thermal–Structure for Hypersonic Vehicles. Aerospace (2021) 8(9):265. 10.3390/aerospace8090265
7.
Kemp NH Riddell FR . Heat Transfer to Satellite Vehicles Re-Entering the Atmosphere. J Jet Propulsion (1957) 27(2):132–7. 10.2514/8.12603
8.
Fay J Riddell FR . Theory of Stagnation Point Heat Transfer in Dissociated Air. AIAA J (2003) 41(7):373–85. 10.2514/8.7517
9.
Lees L . Laminar Heat Transfer over Blunt-Nosed Bodies at Hypersonic Flight Speeds. J Jet Propulsion (1956) 26(4):259–69. 10.2514/8.6977
10.
Bong-Ryul Y Lee S-B . A Critical Review on Multiaxial Fatigue Assessments of Metals. Int J Fatigue (1996) 18(4):235–44. 10.1016/0142-1123(96)00002-3
11.
Bigdeli B Lu FK . Hypersonic, Turbulent Viscous Interaction Past an Expansion Corner. AIAA J (1994) 32(9):1815–9. 10.2514/3.12178
12.
Qu F Sun D Zuo G Shi Y . An Improvement on the Ausmpwm Scheme for Hypersonic Heating Predictions. Int J Heat Mass Transfer (2017) 108:2492–501. 10.1016/j.ijheatmasstransfer.2016.12.031
13.
Zhao R Wen CY Tian XD Long TH Yuan W . Numerical Simulation of Local Wall Heating and Cooling Effect on the Stability of a Hypersonic Boundary Layer. Int J Heat Mass Transfer (2018) 121:986–98. 10.1016/j.ijheatmasstransfer.2018.01.054
14.
Pandolfi M D’Ambrosio D . Numerical Instabilities in Upwind Methods: Analysis and Cures for the “Carbuncle” Phenomenon. J Comput Phys (2001) 166(2):271–301. 10.1006/jcph.2000.6652
15.
Chen Z Huang X Ren Y-X Zhou M . General Procedure for Riemann Solver to Eliminate Carbuncle and Shock Instability. AIAA J (2017) 55(6):2002–15. 10.2514/1.j055366
16.
Mark PG . Static and Aerothermal Tests of a Superalloy Honeycomb Prepackaged Thermal Protection System. Washington, DC: NASA, Scientific and Technical Information Program (1993). 3257. Available from: https://ntrs.nasa.gov/citations/19930014907.
17.
Scott CD . Effects of Nonequilibrium and Wall Catalysis on Shuttle Heat Transfer. J Spacecraft Rockets (1985) 22(5):489–99. 10.2514/3.25059
18.
Candler GV . Next-Generation Cfd for Hypersonic and Aerothermal Flows. In: 22nd AIAA Computational Fluid Dynamics Conference; 2015 June 22–26; Dallas, TX (2015).
19.
Yamamoto Y Kai T Hozumi K . Numerical Rebuilding of Aerothermal Environments and Cfd Analysis of Post Flight Wind Tunnel Tests for Hypersonic Flight Experiment Hyflex. In: 35th AIAA Thermophysics Conference; Anaheim, CA; June 11–14 2001 (2001).
20.
Viquerat J Meliga P Larcher A Hachem E . A Review on Deep Reinforcement Learning for Fluid Mechanics: An Update. Phys Fluids (2022) 34(11):111301–11. 10.1063/5.0128446
21.
Ding D Chen H Ma Z Zhang B Liu H . Heat Flux Estimation of the Cylinder in Hypersonic Rarefied Flow Based on Neural Network Surrogate Model. AIP Adv (2022) 12(8). 10.1063/5.0108757
22.
Ren H Wang S Yuan X Chen J Zhang Y Xiang X . A Flight Test Based Deep Learning Method for Transition Heat Flux Prediction in Hypersonic Flow. Phys Fluids (2022) 34(5):2022. 10.1063/5.0093438
23.
Minsky M Papert S . An Introduction to Computational Geometry. Cambridge tiass., HIT (1969) 479(480):104.
24.
Krizhevsky A Sutskever I Hinton GE . Imagenet Classification with Deep Convolutional Neural Networks. Adv Neural Inf Process Syst (2012) 25. 10.1145/3065386
25.
Du Q Li Y Yang L Liu T Zhang D Xie Y . Performance Prediction and Design Optimization of Turbine Blade Profile with Deep Learning Method. Energy (2022) 254:124351. 10.1016/j.energy.2022.124351
26.
Zhang X Zhang P Peng B Yi X . Prediction of Icing Wind Tunnel Temperature Field with Machine Learning. J Experiments Fluid Mech (2022) 36(5):8–15. 10.11729/syltlx20210196
27.
Bhatnagar S Afshar Y Pan S Duraisamy K Kaushik S . Prediction of Aerodynamic Flow Fields Using Convolutional Neural Networks. Comput Mech (2019) 64:525–45. 10.1007/s00466-019-01740-0
28.
Yuan J Wengang Z Lei Z Qiang LI Haoyuan ZHANG Lin J . Cnn-Based Method for Predicting Aerodynamic Heating. Acta Aerodynamica Sinica (2023) 42(1):13–25. 10.7638/kqdlxxb-2023.0072
29.
Dai G Zhao W Yao S Chen W . Deep-Learning Strategy Based on Convolutional Neural Network for Wall Heat Flux Prediction. AIAA J (2023) 61(11):4772–82. 10.2514/1.j062879
30.
Paul N Poëtte G Lugato D Simon P Congedo PM . Accelerating Hypersonic Reentry Simulations Using Deep Learning-Based Hybridization (With Guarantees). J Comput Phys (2024) 498:112700. 10.1016/j.jcp.2023.112700
31.
Gkimisis L Dias B Scoggins JB Magin T Mendez MA Turchi A . Data-Driven Modeling of Hypersonic Reentry Flow with Heat and Mass Transfer. AIAA J (2023) 61(8):3269–86. 10.2514/1.j062332
32.
Nagendra SKG Maheshwari NK . Multi-species Compressible Solver for Non-Continuum Flow through a Micro-Channel. Int J Comput Fluid Dyn (2022) 36(3):207–31. 10.1080/10618562.2022.2091776
33.
Garbacz C Morgado F Fossati M Maier WT Munguía BC Alonso JJ et al Parametric Study of Nonequilibrium Shock Interference Patterns over a Fuselage-And-Wing Conceptual Vehicle. AIAA J (2021) 59(12):4905–16. 10.2514/1.j060470
34.
Economon TD Palacios F Copeland SR Lukaczyk TW Alonso JJ . Su2: An Open-Source Suite for Multiphysics Simulation and Design. Aiaa J (2016) 54(3):828–46. 10.2514/1.j053813
35.
Taud H Mas J-F . “Multilayer perceptron (MLP),” in Geomatic approaches for modeling land change scenarios (Heidelberg, Germany and New York, United States: Springer International Publishing) (2017). 451–5.
36.
Abien Fred Agarap. ArXiv, abs/1803.08375. Deep Learn using rectified linear units (Relu) (2018).
37.
Alzubaidi L Zhang J Humaidi AJ Al-Dujaili A Duan Y Al-Shamma O et al Review of Deep Learning: Concepts, Cnn Architectures, Challenges, Applications, Future Directions. J big Data (2021) 8:53–74. 10.1186/s40537-021-00444-8
38.
Zhao Y Wang G Tang C Luo C Zeng W Zha Z-J . A Battle of Network Structures: An Empirical Study of Cnn, Transformer, and Mlp. arXiv preprint arXiv:2108.13002 (2021).
39.
Ben Driss S Soua M Kachouri R Mohamed A . A Comparison Study between Mlp and Convolutional Neural Network Models for Character Recognition. In: Real-Time Image and Video Processing 2017. Anaheim, CA: SPIE - International Society for Optics and Photonics (2017). 32–42.
40.
Klopfer G Yee H . Viscous Hypersonic Shock-On-Shock Interaction on Blunt Cowl Lips. In: 26th Aerospace Sciences Meeting, 233 (1988).
41.
Knight D Longo J Drikakis D Gaitonde D Lani A Nompelis I et al Assessment of Cfd Capability for Prediction of Hypersonic Shock Interactions. Prog Aerospace Sci (2012) 48:8–26. 10.1016/j.paerosci.2011.10.001
42.
Maier WT Needels JT Garbacz C Morgado F Alonso JJ Fossati M . Su2-nemo: An Open-Source Framework for High-Mach Nonequilibrium Multi-Species Flows. Aerospace (2021) 8(7):193. 10.3390/aerospace8070193
43.
Nompelis I Candler GV Maclean M Wadhams TP Holden MS . Numerical Investigation of Double-Cone Flow Experiments with High-Enthalpy Effects. In: 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition; 2010 January 04–07; Orlando, Florida (2010).
Summary
Keywords
aerothermal heating, heat flux, numerical simulation, multilayer perceptron, convolutional neural network
Citation
Wang Y, Huang Y, Zhou H, Wang Y, Ji T and Xie F (2025) Prediction of Aerothermal Heating: From Numerical Simulations to Machine Learning Models. Aerosp. Res. Commun. 3:14274. doi: 10.3389/arc.2025.14274
Received
30 December 2024
Accepted
14 February 2025
Published
26 February 2025
Volume
3 - 2025
Updates
Copyright
© 2025 Wang, Huang, Zhou, Wang, Ji and Xie.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fangfang Xie, fangfang_xie@zju.edu.cn
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.